Indice del volumen
Volume index
Comité Editorial
Editorial Board
Comité Científico
Scientific Committee
TOWARDS THE ESTIMATION OF THE FRACTAL DIMENSION OF HEART RATE VARIABILITY DATA.
Hernández Cáceres JL, Foyaca Sibat H, Hong R, Garcia L, Sautié M, Namugowa V.
Department of Physiology and Department of Neurology,
CECAM-ISCMH Cubanacan. Havana, Cuba. University of Transkei. Umtata. South Africa
Rev Electron Biomed / Electron J Biomed 2004;1:4-15.
- The FDH according to the definition provided by Higuchi2.
- The Long Range Slope (LRS) index, a measure of self-similarity obtained from time-detrended signals13,14.
- The Autoregressive Dimensional Index (ARDI), obtained from the application of non-linear non-parametric identification analysis to HRV data15.
Even when related to each other, each index is based on a different theoretical grounding.
Prior to the FD estimation from HRV data, numerical experiments were carried out with each of the above-mentioned indices to find:
- The functional relationship between FDH and power law index of synthetic signals whose length was comparable to that of 2-hour HRV data. This was done to confirm that FDH is a reliable FD estimate that can be applied to real HRV signals.
- The other two Ix’s were compared to FDH to demonstrate their usefulness in FD estimation.
- The robustness of FD estimates obtained using each method with respect to the presence of non-fractal components in the time series.
We concluded that all the three indices had similar performance for estimating the FD of a time series.
The separate use of each of these indices, as well as their combined use seems to be recommendable for the study of fractal time series with unknown FD. The FD was estimated from HRV traces downloaded from the "Fantasia" database. A set of ten HRV recordings corresponding to 5 young (Y) and 5 elderly (O) clinically healthy male humans was used. We obtained that FD values estimated using each of the three indices, were lower in the group of elderly subjects, when compared to their young counterparts. This is in agreement with data from literature and points to the utility of all the three indices.
MATERIALS AND METHODS
Data Sets
Simulated data: For generating a time series with a known FD value, the methodology introduced by Higuchi2 was followed. For that purpose, Inverse Fourier Transforms (IFTs) were applied to vectors with random phases and spectral densities following (3).
For further details about the procedure for generating fractal time series Higuchi’s article2 is advised.
By conveniently changing the power law index, a set of simulated signals with FD values ranging from FD = 1.5 to FD = 1.95 was submitted to further analysis.
Non purely fractal synthetic signals.
For estimating the influence of non-fractal sources into the different FD, a fractal signal with FD = 1.85 was mixed at different proportions by adding to it a non-fractal signal whose spectrum was non-zero only at F=3000, and was zero elsewhere. The contribution of the non-fractal signal was measured in proportions of total variance. It ranged from 0% to 29% (see table I)
HRV data
The database included 10 recordings of intervals between ECG R-waves (I-RR), corresponding to 5 young subjects aged between 21-34 years old (Y), and 5 elderly, 68-81 year old subjects (O). All subjects were rigorously screened and a healthy condition was certified. ASCII files with individual recordings (< O1.txt >, < Y1.txt >,…, etc.) were downloaded from the "Fantasia" database, freely available at "http://www.physionet.org". Details about the "Physionet" website, as well as about the possibility to use these data for research purposes are described in Iyengar’s manuscript11.Each trace corresponded to an I-RR signal obtained from 2 hours of continuous ECG recording in a supine position, and contained at least 4000 heartbeat counts. The authors11 provide a further description of the data.
Signal Analysis.
The following indices were estimated from purely fractal and from non-purely fractal simulated traces, as well as from real HRV data.Fractal Dimension Following Higuchi’s method FDH.
Higuchi2 proposed a method to calculate the fractal dimension of self-similar curves in terms of the slope of the straight line that fits the length of the curve versus the time interval (the lag) in a double logarithmic plot. The method consist of considering a finite set of data taken at intervals v (1), v (2), …, v (N). From this series it may be constructed a new series v(m,k), defined as:v(m), v(m+k), v(m+2k),…,v(m+[(N-m)/k].k) ; with m=1,2,…,k. (5)Where "[ ]" is the integer part, i.e. [x] is the largest integer a such that a <x, and m, k are integers that indicate the initial time and the time interval respectively. The length of the curve v(m,k) is defined as
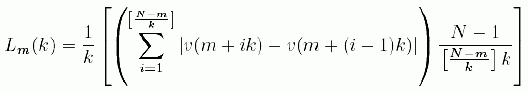 (6)
(6)Then, the length of the curve for the time interval k is given by Lm = meank[Lm(k)], the average over k sets Lm(k). Finally, if mean(L(k)) is proportional to kD, then the curve is fractal with fractal dimension D. We call this estimate FDH
Long Range Slope (LRS). LRS is one of the parameters estimated during detrended fluctuation analysis (DFA)14. The overall idea of the method is to estimate the roughness of a time series that was previously corrected for any local linear trend. In our version the time series to be analysed is divided into boxes of equal length, n. In each box of length n, a least-squares line is fit to the data (representing the trend in that box). Next, the time series is detrended by subtracting the local trend in each box. Then the detrended time series is integrated. The root-mean-square fluctuation of this integrated and detrended time series is calculated and denoted as F (n).
This computation is repeated over all time scales (box sizes), from n = minbox to n = maxbox, to characterize the relationship between F (n), the average fluctuation, and n, the box size. Typically, F (n) will increase with box size n. A linear relationship on a log-log plot indicates the presence of power law (fractal) scaling. Under such conditions, the fluctuations can be characterized by a scaling exponent, i.e., the slope of the line relating log [F (n)] to log [n]. It has been shown that in HRV16 data, instead of a continuous line, we observe two lines with a breakpoint. One line correspond to short duration boxes (e.g. n<5), whereas the second corresponds to boxes with n>7. The slope of the long-range segment (LRS) was considered in our computations, with n ranging from n = <minbox=14> to n = <maxbox=64>.
There is one difference between our procedure and that of the classical DFA method13. In the original version, the signal is integrated prior to be detrended. However, our version proved to have a high predictive power while assessing haemodynamic instability among haemodialysis patients from their HRV data14.
Autoregressive Dimension Index (ARDI). Enzmann et al15 firstly introduced this index as a measure for evaluating HRV in patients under haemodialysis treatment. The rationale of the method is to apply a non-linear identification approach to no stationary data. Non-linear identification has proven to be adequate for the analysis of short duration (180-500 data points) time series whose dynamical nature is unknown17. The method allows separating the deterministic and stochastic components of a stochastic non-linear system. In particular, most of the known classical chaotic attractors could be reproduced by this method17. It can be viewed as an extension of classical linear autoregressive estimation to the non-linear case, but also as an extension of classical chaos theory approach to the case when the non-linear system is fed by innovation noise18,19. From all the wealth of information that is obtained by this method we selected a single parameter, namely, the optimal order of the autoregressive model.
For ARDI estimation a recording of duration N = 400 was divided into 20 non overlapping segments 200 data points long each. To each segment the following non-linear autoregressive model was fit:
I n = f(I n-1,In-2,…,In-m) +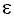 n (7)
n (7)Where I n-1 , l n-2 ,…,I n-m are the z n-1, z n-2,…,z n-m R-R intervals in the sequence.
f is a multivariate non-linear function relating the nth interval to the k preceding intervals in the sequence. Under our assumptions, {
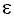 n } corresponds to a random, independent, identically distributed variable. The parameter m is the order of the non-linear autoregressive model. The function f is estimated non-parametrically20.
n } corresponds to a random, independent, identically distributed variable. The parameter m is the order of the non-linear autoregressive model. The function f is estimated non-parametrically20.
According to this method, the estimate at an arbitrary point (Zt-1, Zt-2,…Zt-m) of the state space is obtained as a weighted average of the data.
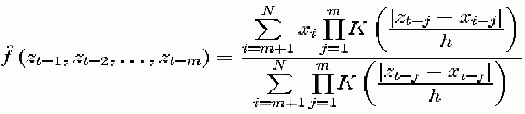 (8)
(8) The bandwidth parameter h determines the weight of each neighbouring point in the phase space. In particular, if h is too large we have just averaging, whereas for a too small h noise will be incorporated into the deterministic function. A minimal cross validation error criterion has been used for selecting the bandwidth parameter17,18,19. The determination of the optimal order of an autoregressive model is a difficult task even for parametric models. The introduction of likelihood criteria is an attempt to penalize the good prediction at expenses of too many parameters. For that purpose a cross validation criterion has also being used17,18,19. For a description of the use of cross validation in kernel non-linear nonparametric auto regression the reader is referred to21.
After computing the optimal order m for each segment of the whole trace it is possible to compute ARDI as the proportion of m-values equal or higher than 15 corresponds to ARDI.
ARDI = Number of segments with optimal order higher than 15
Total number of segments.Estimation of fractal dimension via index evaluation.
For estimating the fractal dimension on the basis of a particular index (FDIX), NE was carried out. FDLRS, and FDARDI were considered, whereas FDH was taken as the reliable reference value ("golden standard"), otherwise it is assumed that FDH is identical to FD.
At least 10 simulated signals with FD ranging from FD=1.5 to FD=1.95 were submitted to the estimation of each index.
The dependence of FD respect to each Ix was fit to a polynomial
FD =Pl (Ix) (9)Where l is the degree of the polynomial P.
Accordingly, the FD of a given time series was obtained via estimating each index and applying (9). Linear regression was used for estimating FDLRS, and 2nd degree polynomial fit was used for FDARDI. For the estimation of the polynomial coefficients as well as their standard errors, the "Statistica" package was used.
Statistical analysis
Mean and standard deviation for FDH, FDLRS and FDARDI were obtained for both Y and O groups. Both parametric analysis under a Gaussian assumption (one-sided t-test) and non-parametric analysis were undertaken.
Nonparametric permutation analysis is recommended for small samples with unknown distribution22 for each index, all the 10 individual values from the Y and O traces were allocated according to all possible permutations into 2 groups with 5 individuals each. The difference between the mean values for each randomly generated pair of groups was computed. An empirical distribution for the differences between the means was generated. Accordingly, the probability for the mean difference between Y and O the corresponding null hypothesis (H0) of no differences was estimated following an area-under-the-curve criterion.
RESULTS
A. Numerical experiments.
Our first task was to reproduce the numerical experiments performed by Higuchi2 for the case when the duration of the segment is relatively short (N=4000). We obtained that in the Power Law Index (
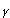 ) values region from 1.2 to 1.8 the FDH values corresponded nicely to the theoretically expected relationship (2). Our regression yielded:FDH=2.48- 0.46
) values region from 1.2 to 1.8 the FDH values corresponded nicely to the theoretically expected relationship (2). Our regression yielded:FDH=2.48- 0.46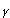 (n=87, r=0.97); (10)
(n=87, r=0.97); (10)
Thus we regard this result as supporting the validity of FDH as an estimate for FD.
Previous results from our laboratory suggested that FD values for HRV data are expected in the 1.1 - 1.9 values region. In order to find out the relationship between each index and FD, we carried out statistical analysis under the polynomial model
FD=a0+a1(x)+a2(x2) (11)where x=LRS, ARDI, and a0, a1 and are the coefficients to be estimated. As the result of the NE carried out, the values for the respective coefficients are presented in table I.
Rewieved by Dr Douglas R McLean Department of Computing Science and Mathematics University of Stirling. Stirling, Scotland. UK
Rewieved by Antonio Núñez Reiz MD.Medicina Intensiva. Hospital Fundación de Alcorcón. Madrid, España
Key Words: Heart rate variability; fractal dimension.
ABSTRACT
With the aim of determining the Fractal Dimension (FD) of Heart Rate Variability (HRV) signals, three indices (Ix) were evaluated using HRV data. The relationship between each (Ix) and FD was established via a Numerical Experiments (NE) approach. Signals with known FD, were evaluated using different Ix. Once the functional relationship between FD and Ix was found, an estimate of the FD, based on a particular Ix can be proposed (FDIx).
The following Ix’s were analysed: A) Fractal Dimension estimated by Higuchi’s method (FDH); B) Long Range Slope (LRS), obtained from time detrended data, as well as C) the Autoregressive Dimension Index (ARDI) a measure recently proposed by Enzmann et al for evaluating HRV data. Our results showed that, for fractal signals, a statistically sound functional dependence between FD and each of the other two Ix’s was found for 1.5-1.95 FD values region. Adding non-fractal components to a pure fractal signal increased FDIx. The three indices behaved similarly, i.e. 5-7 % FDIx increase in the presence of about 30% of non-fractal contribution.
A comparison between FDIx of old vs. young subjects revealed a reduction in the FD of the elderly. This is in agreement with literature data, and points to the adequacy of the three methods here proposed.
INTRODUCTION
Fractals are figures and objects that are self-containing in recursive fashion. Fractals can be generated by recursive application of mathematical functions. Any part of the object is a replica of the whole object, but of a smaller size, to infinitesimal levels. The recursive nature of fractals and how close they resemble natural elements make it an important facet to mathematics and computer graphics. Not only geometrical figures behave as fractals, but also mathematically generated time series behave in a self-similar way. Certain real world processes such as earthquakes, river flooding or even Brownian motions1 do share many properties of fractal time series. To characterize the entire complex behavior of a fractal in quantitative terms is a major goal in this area. One of the simplest ways to do so is by fractal dimension (FD) estimation.
For a smooth (i.e., nonfractal) line, an approximate length L(r) is given by the minimum number N of segments of length r needed to cover the line: L(r)=Nr. As r goes to zero, L(r) approaches a finite limit, the length L of the curve. Similarly one can define the area A or the volume V of nonfractal objects as the limit of an integer power law of r:
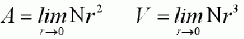 (1)
(1) Where the integer exponent is the Euclidean dimension E of the object.
This definition cannot be used for fractal objects: as r tends to 0, we enter finer and finer details of the fractal and the product NrE may diverge to infinity. However, a real number D exists so that the limit of NrD stays finite. This exponent provides an illustration of what the fractal dimension (FD) is. A commonly used practical way to estimate the fractal dimension is the so-called box counting dimension1:
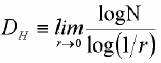 (2)
(2)In the frequency domain, fractal time series exhibit power law properties:
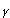 (3)
(3)Where Psd is the power spectral density, f is the frequency and the exponent A time series with random phases and power spectrum following the property (3) may be regarded as a synthetic signal with known fractal dimension. Higuchi2 generated synthetic signals with different values of A common problem in analyzing fractal properties of heart rate variability data emerges from the fact that the HRV signal is not a purely fractal process3. Available spectral methods4 present (besides other) the drawback that some FD values from real subjects are beyond the linearity region where (4) is valid (see our results below). Besides, the robustness of FDH in presence of nonfractal components has not been evaluated so far.
It seems plausible to propose estimates of FD based on different approaches. This perhaps can reduce any method-related bias. At the same time, agreement between methods when real data are being evaluated, as well as providing sense-making differences between groups of subjects may further support their use.
The importance of Heart Rate Variability is in providing a non-invasive and reliable means to assess autonomic nervous function. Heart rate is primarily controlled by the balance between parasympathetic and sympathetic nervous system acting on the intrinsic pacemaker discharge frequency of the sinoatrial node. The normal intervals between heart beats, (only a small fraction of the entire ECG signal) contains a great deal of information about intracardiac and extracardiac processes including its active function controlled by the autonomic nervous system (ANS) as before-mentioned, therefore the heart rate variability (HRV) is an objective procedure used in medicine, especially in the domain of disorders of ANS. A robust HRV research finding is that it is the best predictor of sudden death4 and for mortality from numerous and diverse medical causes4. Its clinical relevance was appreciated when was confirmed that foetal distress was preceded by alterations in interbeat intervals before any appreciable change occurred in the heart rate itself5.
Because HRV can show the status of the autonomic nervous system, it can indicate the early degree of deterioration of the ANS in diabetes mellitus6, HIV/AIDS, Guillain-Barré syndrome, orthostatic hypotension of the Shy-Drager type in parkinsonism, multiple sclerosis, behavioral disorders, brain injury, as well as in chronic alcoholism, and other possible degenerative neurological conditions4. HRV also can be used as a simple tool for monitoring therapeutic effectiveness, and it has become known as a death predictor7.
Besides the well-documented relationship between HRV parameters and ANS, there are ample evidences about the presence of fractal properties in the HRV signal3,7,8, 9, 10,11,12. Even when the research on this field is not recent, literature about HRV fractal properties sometimes is contradictory. Besides, hitherto we do not have a physiological counterpart for the putative fractal properties changes observed in different groups of patients. It is our opinion that we need reliable ways of confirming and characterizing the fractal properties of HRV. In this paper, we rely on a numerical experiments approach, where different indices are calculated from synthetic signals whose fractal dimension is known. The original data were "corrupted" with the presence of nonfractal components in order to explore the robustness of these indices for FD assessment.
In this work we studied three different indices for evaluating the FD in a set of HRV traces:
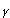 is the so-called power spectral index 2,3. For the values region between FD=1.1 and FD = 1.8 the following relationship between FD and
is the so-called power spectral index 2,3. For the values region between FD=1.1 and FD = 1.8 the following relationship between FD and 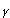 is valid2:
is valid2:
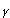 )/2 (4)
)/2 (4)
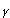 (and correspondingly different FD values). This allowed him to propose a reliable method for fractal dimension estimation (FDH).
(and correspondingly different FD values). This allowed him to propose a reliable method for fractal dimension estimation (FDH).
Coefficients of the polynomial regression under the model (11) found for the dependence of FD upon LRS and ARDI. Standard errors of the coefficients are provided.
| x | a0 | a1 | a2 | n | Variance explained |
| LRS | 2.1193 ± 0.0034 | -0.9995 ± 0.014 | 0 | 10 | 99.90% |
| ARDI | 1.9154 ± 0.0047 | 0 | -0.000021 ± 0.000001 | 100 | 87% |
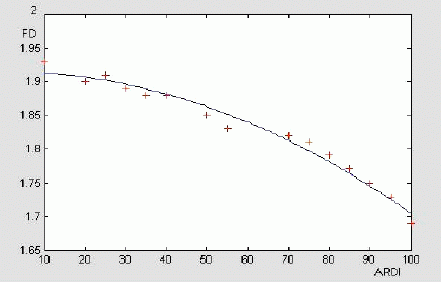
The relation between ARDI and FD is illustrated in fig (1).
FDLRS, and FDARDI are obtained from (11) with the respective coefficients provided in Table I. respectively.
The degree of concordance between different FD estimates was high when purely fractal signals were evaluated, thus for FDARDI and FDH the correlation coefficient was r = 0.96 (n=10).
Addition of a non-fractal signal to a purely fractal signal was a cause for FD increase with all the three indices. As shown in table I adding up to about 30% of a non-fractal component to the total variance increases the estimated FD value in about 5-7%. According to different authors, in HRV data from healthy subjects about 22% of the total variance is increased by nonfractal components3. At the same time, it seems plausible to expect that most of the clinical conditions related to changes in the spectral peaks (LF, and HF) imply changes in the range from the "normal" value of 22% to lower values around 18 %4. Following the results shown in table I, it means that changes in nonfractal spectral peaks may not account for more than a 1% change in FD values estimated by any of these indices. Thus, our results suggest that all the three proposed FD estimates might be pertinent for HRV fractal dimension evaluation.
Table II
Percent change in different FD as results of adding a non-fractal component to a purely fractal signal whose fractal dimension was FD = 1.85. Here, "100%" correspond to that value of FD=1.85 with a zero nonfractal contribution.
| % non fractal variance added | FDPLI | FDLRS | FDARDI |
| 0 | 100 | 100 | 100 |
| 1 | 100 | 101 | 100 |
| 10 | 102 | 102 | 101 |
| 16 | 105 | 105 | 108 |
| 29 | 105 | 106 | 107 |
HRV data: In table III the estimates of FD according to each index are shown for each of the HRV recording analysed.
Table III
FD values for the 10 recordings from the "Fantasia" database. Recording’s codes correspond to the original file names as presented at the website.
| Recording’s code | FDPLI | FDLRS | FDARDI |
| 01 | 1.64 | 1.85 | 1.61 |
| 02 | 1.49 | 1.5 | 1.34 |
| 03 | 1.46 | 1.45 | 1.36 |
| 04 | 1.62 | 1.88 | 1.49 |
| 05 | 1.78 | 1.9 | 1.66 |
| Y1 | 1.11 | 1 | 1.11 |
| Y2 | 1.47 | 1.15 | 1.29 |
| Y3 | 1.36 | 1 | 1.46 |
| Y4 | 1.29 | 1.22 | 1.29 |
| Y5 | 1.36 | 1.3 | 1.31 |
In table IV, a summary is provided for the statistical processing of the data.
Means standard deviations and type I error probabilities for the groups O and Y. for estimating PI a one-sided t-test criterion was followed. In the case of permutations the probability P0 that the difference between the means of the both groups is zero has been computed (proportion of area under the curve criterion)..
| Group | FDH | FDLRS | FDARDI |
| Y | 1.8730 ± 0.04 | 1.9167 ± 0.0177 | 1.8837 ± 0.0360 |
| O | 1.7656 ± 0.077 | 1.7403 ± 0.0688 | 1.8080 ± 0.06 |
| PI (Gaussianity assumption) | 0.0002 | 0.0003 | 0.0215 |
| P0(Permutations) | 0.004 | 0.004 | 0.0197 |
According to the three indices considered FD is decreased in the group of elderly subjects. Statically significant differences were obtained using either conventional or nonparametric permutation analysis. These results agree with ample literature evidence mainly using other FD estimation methods11.
DISCUSSION
Here three indices for time domain estimation of FD in HRV data were proposed. Higuchi had previously proposed one of these indices (FDH). The second index (LRS) is a modification of the original DFA method. DFA indices often are used for statistical discrimination between groups of patients. In particular our group has used LRS for few years. Even when recognized that DFA indices are related to some properties of fractal signals, this is, to our knowledge, the first attempt to use one of these indices for FD estimation. The third index (ARDI) appeared from our early attempts to characterize HRV by a non-linear identification approach23.
As our result revealed, the two indices are functionally related to fractal dimension when purely fractal signals were analysed. The "robustness" of all three indices was similar when purely fractal signals were mixed with nonfractal components. However, we do agree that more specific numerical experiments are needed for a more complete characterization of these indices’ robustness.
All the three indices documented in a similar way a result with ample literature support: the decrease with age of FD from HRV recordings11.
A further step in our research might be the possibility to use these estimates for assessing FD from short duration traces, as well as from traces sampled al lower frequencies. Our preliminary results (not shown) point to a preservation of the predictive power of these estimates even for 2-min duration traces, whereas only one of the indices (FDH) loses its clinical predictability as the sampling frequency is reduced from 1000 to 100 Hz.
Recent experience with the advent of chaos theory shows that we must be extremely cautious when trying to apply results of mathematical theories into real objects. An avalanche of chaos "demystification" followed the early "epidemics" of chaos finding in almost any area of physiology17, and the sad sensation that our understanding of different physiological mechanisms remains obscure had become a reason for pessimism.
In our opinion, the sole use of power spectrum measures for assessing the putative fractality of a time series whose mechanism is unknown may appear misleading. Even with mathematical objects this can take place. One example is the known intermittent Pomeau-Manneville map24. This map is a deterministic non-linear low dimensional process. However, its power spectrum is undistinguishable from that of a typical fractal with "1/f" noise. The non-linear identification approach (from which ARDI is derived) is capable of distinguishing the both. Thus we may expect that these indices will provide not only new ways for assessing HRV fractal properties, but also for understanding some of HRV underlying dynamics.
The fractal properties of HRV may open avenues for radically new promising views to the heart beat regulation. Concepts such as self-organized criticality increase our understanding of physiological regulatory mechanisms not encased in the classical framework of the feedback theory scenario25, 26. However, for these views being productive, we need a simple conviction: that fractal-like processes take place in the human body. Our work has been an attempt in that direction. On the other hand, there is no doubt regarding the presence of feedback mechanisms, very likely non-linear, acting as result of the influences of the both branches of the Autonomic Nervous System. To quantitatively handle HRV in a framework that includes all of these processes is a major task.
FIGURE CAPTIONS
Figure 1. Relationship between FD and ARDI. Data corresponds to the Fractal Dimension evaluated from a simulated signal whose ARDI had been previously estimated. The solid line is calculated on the basis of the coefficients provided in table I (100 data points). Each dot is the average of at least three NE replicate.
Acknowledgements. We thank to Ms Allison Swanby for discussing the paper as well as for redaction corrections. Especially we thank an unknown referee that managed to be strict and encouraging at the same time.
REFERENCES
1.- B. B. Mandelbrot The fractal Geometry of Nature, Freeman, New York, 1982
2.- Higuchi, T., Relationship between the fractal dimension and the power law index for a time series: A numerical investigation, Physic D. 1990; 46: 254-264.
3.- Yamamoto Y and R. L. Hughson, Coarse Graining spectral analysis: new method for studying heart rate variability. J. Appl. Physiol. 1991,71(3): 1143-1150.
4.- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation. 1996;93:1043-1065.
5.- F. Williams KP, Galerneau Fetal heart rate parameters predictive of neonatal outcome in the presence of a prolonged deceleration. - Obstet Gynecol. 2002;100:951-959
6.- A. Al-Hazimi, N. Al-Ama, A. Syarnic, R. Qosti, K. Abdel-Galil. Time domain analysis of heart rate variability in diabetic patients with and without autonomic neuropathy. Annals of Saudi Medicine. 2002;22 (http://www.kfshrc.edu.sa/annals/html/toc225_226.html).
7.- Tapanainen JM, Thomsen PE, Kober L, Torp-Pedersen C, Makikallio TH, Still AM, Lindgren KS, Huikuri HV. Fractal analysis of heart rate variability and mortality after an acute myocardial infarction. Am J Cardiol. 2002;90:347-352.
8.- Goldberger, A. L., D. R. Rigney. Defending against sudden death: Fractal mechanisms of cardiac stability. Proc. 9th Ann. IEEE/EMBS Conference 1987;1313.
9.- Koshino T, Kimura Y, Kameyama Y, Takahashi T, Yasui T, Chisaka H, Sugawara J, Okamura K. Fractal and periodic heart rate dynamics in fetal sheep: comparison of conventional and new measures based on fractal analysis. Am J Heart Circ Physiol. 2003;284:1858-1864.
10.- Francis DP, Wilson K, Georgiadou P, Wensel R, Davies LC, Coats A, Piepoli M. Physiological basis of fractal complexity properties of heart rate variability in man.J Physiol. 2002;542:619-629.
11.- Iyengar N, Peng CK, Morin R, et al. Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am J Physiol 1996;271:1078-1084.
12.- Peng C-K, Havlin S, Stanley HE, Goldberger AL. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995;5:82-87.
13.- Peng C-K, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic organization of DNA nucleotides. Phys Rev E. 1994;49:1685-1689.
14.- Luis Garcia Dominguez (J. L. Hernandez Caceres y Guido Enzmann como tutores) Aplicacion del Metodo de DFA al estudio de la Variabilidad de la Frecuencia cardiaca en pacientes de Hemodialisis. CECAM, La Habana, 2000.
15.- Enzmann G, Garcia Lanz A, Hernandez Caceres JL, Garcia Dominguez L, Gonzalez A. Un nuovo indice di complessita per la valutazione della variabilita della frequenza cardiaca in pazienti in trattamento emodialitico. In: Timio M, Wizemann V, Venazi S (Eds) Cardionefrology Ed. Bios, Roma, 1999. 283-285.
16.- Peng C-K, Hausdorff JM, Goldberger AL. Fractal mechanisms in neural control: Human heartbeat and gait dynamics in health and disease. In: Walleczek J, ed. Nonlinear Dynamics, Self-Organization, and Biomedicine. Cambridge: Cambridge University Press, 1999.
17.- Valdés S P, Bosch J, Jiménez J C, Trujillo N, Biscay R, Morales F, Hernández-Caceres J L, Ozaki T. The statistical identification of non-linear brain dynamics: A progress report. In: Non-linear Dynamics and Brain Functioning. Pradhan N., Rapp P.,Sreenivasan E. (Eds.), Nova Science Publishing. 1999,278-284.
18.- Hernandez Caceres JL, Biscay R, Grave de Peralta R, Jimenez JC: Measuring the dissimilarity between EEG recordings through a non-linear identification approach. Int J. Biomed Computing. 1994;26:256-262.
19.- Hernandez Caceres JL, Valdes S P,Vila P: The spike and wave EEG activity modelled as a stochastically perturbed limit cycle. NeuroReport. 1996;28:164-170.
20.- Tjostheim D, Auestad B. Nonparametric identification in non-linear time series: Projections. JASA 1994;79:1398-1402.
21.- Haerdle W (1993) Applied Nonparametric Regression. Cambridge University Press.
22.- Diacons P. Efron B. Computer-Intensive methods in statistics. Sci Amer 1983;248: 96-108.
23.- Hernandez Caceres JL, Garcia Dominguez L, Enzmann G &Garcia Lanz A.(1999) La regulacion autonomica del intervalo cardiaco como un sistema no lineal estocastico con multiples atractores. Revista CENIC Ciencias Biologicas. 30:180-186.
24.- Pomeau, Y. & Manneville, P. Intermittent transition to turbulence in dissipative dynamical systems. Commun Math Phys. 1980;74:189-197.
25.- Bak P, Chen K. Self-organized criticality. Sci Amer. 1991;246:46-53.
26.- West BJ. Physiology in fractal dimensions: error tolerance. Ann Biomed Eng. 1990;18: 135-149.
Comment by Douglas McLean. Department of Computing Science and Mathematics University of Stirling. Stirling, Scotland. UK drm@cs.stir.ac.uk
I am now satisfied that the authors have answered sufficiently my queries and recommend it for publication in The Electronic Journal of Biomedicine. The work deals with the estimation fractal dimension from heart rate variability data. The work is new and interesting in that these indices have not been applied in this context before. Their work allows HRV to be characterised as a part fractal, part deterministic signal.
The practical benefits to medicine afforded by this understanding should be pursued and, perhaps the authors would like to mention or speculate as to how the indices might be employed in a clinical context in their discussion.
Comment by Antonio Núñez Reiz. Unidad de Investigación. Hospital General Yagüe. Burgos. España anunez at uninet.edu
(Spanish below)
Studying the electrical properties of the heart has forced scientists to enter in a field rather unexplored and unknown for many of us, mixing physiology with mathematics and specially numerical analysis and control engineering. The inherent complexity of the elements composing the system which generates and conducts the electrical impulses in the human heart creates the need to use mathematical tools and investigation methods that has allowed us to capture that complexity and to analyze it in a rigorous way.
For a long time we have known that the heart rate is controlled by the signals which arrive at the heart from the vegetative nervous system, being the variability of the cardiac frequency partially explained by the influence of the sympathetic and parasympathetic nervous system. Pathologies of these systems (Shy-Drager syndrome, multiple sclerosis, diabetic neuropathy, and others) may affect this variability, and can be studied by studying it. Heart rate variability reduction is an effect of the sympathetic predominance and it is associated to a greater mortality, for example in patients at Intensive Care Units.
This study explores the possibility that other factors exist that affect this variability, and it presents the elegant concept of the fractals applied to the description of the electrical cardiac system cardiac. Although something complicated for nonmathematical minds, the fractal dimension of the variability of the frequency cardiac concept can help to complete the list of the factors that influence this variability, and to explain under a deeper perspective the clinical findings.
As described in the article, fractals are figures or objects that are self-contained in a recursive way, so if we observe the figure on greater or smaller scale we will be with seen the same (see Figure 1). The reader can ask "and what has this to do with the variability of the heart rate?". A little patience and everything will be clarified.

Figure 1
Saying that the variability of the cardiac frequency has a fractal component, we are in fact saying that if we measure RR intervals during a period of time in a subject, we will be see variability patterns that repeat themselves if we multiply the period of time by a certain factor. This factor is indeed the fractal dimension of the variability of the cardiac frequency.
There is an anatomical base, that can be observed in the system of connections that compose the Hiss bundle, that could explain the presence of a fractal dimension in the variability of the frequency cardiac. The authors plead for a possible component of automatic control of the system provided by the presence of a fractal component, that could provide advantageous characteristics in absence of a suitable control operation by autonomous system, that is the fundamental component in normal conditions.
Using numerical analysis the authors determine three different indexes to evaluate the fractal dimension of the heart rate variability and its importance to explain this variability, arriving to the conclusion, after applying them to young and older healthy subjects, that the importance of the fractal component of this variability increases with age. Without being able definitively to exclude the possibility that there is an associated numerical calculation bias to this finding, they provide convincing reasons to think that this mechanism may have relevance in the study of pathologies of the heart rate and others like epilepsy.
SPANISH
El estudio de las propiedades eléctricas del corazón nos obliga a adentrarnos en un campo para muchos de nosotros inexplorado, como es el que mezcla la fisiología con las matemáticas y en concreto con el análisis numérico y la ingeniería de control. La propia complejidad inherente a los elementos que componen el sistema de generación y conducción de los impulsos eléctricos en el corazón humano nos obliga a utilizar herramientas y métodos de investigación que nos permitan capturar esa complejidad y analizarla de manera rigurosa.
Desde hace tiempo se sabe que el ritmo cardiaco está controlado por las señales que llegan al corazón desde el sistema nervioso vegetativo, siendo la variabilidad de la frecuencia cardiaca explicable en parte por el influjo de simpático y el parasimpático. Existen patologías de dichos sistemas (síndrome de Shy-Drager, esclerosis múltiple, neuropatía diabética, etc) que se manifiestan con frecuencia a este nivel y que pueden ser estudiadas explorando dicha variabilidad. La reducción en la variabilidad del ritmo cardiaco es un efecto del predominio simpático y se asocia a una mayor mortalidad, por ejemplo en pacientes ingresados en Unidades de Cuidados Intensivos.
El presente estudio explora la posibilidad de que existan otros factores que afecten dicha variabilidad, e nos presenta el elegante concepto de los fractales aplicados a la descripción del sistema eléctrico cardiaco. Aunque algo complicado para mentes no matemáticas, el concepto de dimensión fractal de la variabilidad de la frecuencia cardiaca puede ayudar a completar la lista de los factores que influyen sobre dicha variabilidad, y a explicar de una manera más completa los hallazgos de la clínica.
Como se describe en el artículo, los fractales son figuras u objetos que se autocontienen a si mismos, de tal forma que si observamos la figura a mayor o menor escala nos encontraremos con lo mismo (ver figura 1). El lector puede preguntarse "¿y que tiene esto que ver con la variabilidad del ritmo cardiaco?". Un poco de paciencia y todo quedará aclarado.
Al decir que la variabilidad de la frecuencia cardiaca tiene un componente fractal, estamos en realidad diciendo que si medimos durante un periodo de tiempo los intervalos RR del ritmo cardiaco en un sujeto, nos encontraremos patrones de variabilidad que se repiten si multiplicamos el periodo de tiempo por un factor determinado. Este factor es precisamente la dimensión fractal de la variabilidad de la frecuencia cardiaca.
Existe una base anatómica, que se puede observar en el sistema de conexiones que componen el haz de Hiss, que podría explicar la presencia de una dimensión fractal en la variabilidad de la frecuencia cardiaca. Los autores abogan por un posible componente de auto-control del sistema proporcionado por la presencia de un componente fractal, que podría proporcionar características ventajosas en ausencia de un adecuado funcionamiento del control por parte del sistema autónomo, que es el componente fundamental en condiciones normales.
Mediante el empleo de análisis numérico los autores determinan tres índices diferentes que permiten evaluar la dimensión fractal de la variabilidad del ritmo cardiaco y su importancia para explicar dicha variabilidad, llegando a la conclusión, tras aplicarlos a sujetos sanos jóvenes y mayores, que la importancia del componente fractal de dicha variabilidad aumenta con la edad. Sin poder excluir definitivamente la posibilidad de que haya un artefacto de cálculo numérico asociado a este hallazgo, proporcionan razones convincentes para creer que este mecanismo puede llegar a tener relevancia en el estudio de patologías del ritmo cardiaco e incluso de otras como la epilepsia.
Received: June 5, 2003.
Published: February 1, 2004
