Electron J Biomed 2007;1:21-27. Musso et al. ... HISTOLOGICAL GLOMERULAR PATTERNS AS CHAOTIC ATTRACTORS

CHAOS THEORY

HISTORICAL BACKGROUND AND MAIN CONCEPTS

Classically, Newtonian Physics has studied the linear systems.

These systems are known for the lineal proportionality they keep between cause and effect. The magnitude of the response depends on the same magnitude of the stimulus so that little causes correspond to little consequences and viceversa.

The linear systems have an evident order and their behaviour can be understood by their direct observation, being relatively simple to recognize their constitutive elements.

However, this type of systems are not abundant in Nature but the the chaotic or not linear systems..The first studies on the subject were performed by the French physician Henri Poincaré, at the end of the XIX th. Century. He was the pioneer in understanding that chaos is not a synonym of disorder but of complexity pretending to be disorder.

The chaotic systems are characterized by the following peculiarities:

There is no proportionality between cause and effect, as small stimuli can cause great consequences.
It is not easy to identify the variables that determine the behaviour of the system. This behaviour is determined by the attractors that influence them.
An attractor is the point or group of points towards evolve the system if it has enough to do it. There exist attractors towards normality states as well as towards system alteration (pathological states).
The complex systems are characterized for having many components, and because its behaviour can not be predicted by knowing each of them. They create circuits where the exists end up generating new entries , constituting cyclic systems.
They have the capability of auto -organization and it comes from the re-feeding capability of the system, and not from external aid.

CHAOS AND ENTROPY

The thermodynamics laws established by Rudolf Clausius and Lord Kelvin, determine that entropy (a magnitude that measures the part of energy which can not be used as work) makes the universe prone to energy dissipation and greater disorder.

However, these statements do not explain the appearance of life and its tendency to evolutive diversification and complexity : the successive appearance of cells, tissues, organs, organ systems, etc.

Maxwell tried to solve this incognita through the following hypothesis: if a system fought the dissipation of its own gradient or entropy, it could be explained then how it achieves the maintenance of its complexity. The scientists called this activity "negentropy" or negative entropy. Ilia Prigogine, one of the founders of the Chaos Theory, proposed that the information that fights the entropy is represented by the auto organization of the matter and the acquisition of a complex internal order, as it happens in the chaotic systems. In this way, the evolution of life in harmony with the thermodynamics principles can be explained..

FRACTAL GEOMETRY

Inside the Chaos Theory , we find the geometry of things, from which they intend to explain the strange forms of Nature. In order to do so, the mathematician Benoit Mandelbrot has introduced the Fractal concept, which derives from the Latin "fractus" that means irregular or fragmentized.

We could define the Fractal as a geometric object which basic structure is repeated in different scales. One of its properties is the auto-similarity : if we take a part of it, it contains a shape that replicated a determined number of times leads again to the original shape. Such phenomenon is known as "recursive symmetry".

In this sense, the fractal objects that can not be represented by the Classic or Euclidian Geometry, (circles, squares, etc.) can be represented by iteration or repetition of a basic structure (fractal).

Mandelbrot achieves to explain the shape of many elements in Nature as the case of the marine shores, the mountains , clouds, etc.

The fractal geometry is expressed through algorithms that require a computer to be converted into shapes and structures.

In a fractal structure, it systematically adopt a determined morphology which is the result of a substructure iteration

In the human body, fractal structures have been described in the coronary arteries, cardionector system, cardiac valves, vascular and bronchial tree.

FRACTAL GEOMETRY AND GLOMERULAR STRUCTURE.

Following, we will expose a hypothesis elaborated from the study of nephron photographies and of the glomerulus in particular, in healthy and sick histological samples.

In the present study we propose that the nephron would follow a fractal shape whose primary structure would be the sinusoidal mathematical function (sine-cosine).

The repetition (iteration) of the sinusoidal mathematical function, with different variations for each nephronal region (Bowman capsule, convoluted tubules, etc.) permits the construction of a complete nephron. (Figure 1).

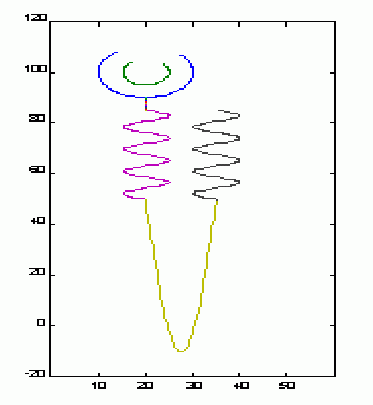
Figure 1

We also noticed that some glomerular histological patterns, that are developed in the context of diverse illnesses, could be variations of the same mathematical function.

That is the case of the morphological patterns of the membranous nephropathy: spike formation (Figure 2), mesangiocapillary glomerulonephritis: double contour (Figure 3) and crescentic glomerulonephritis: crescents (Figure 4).

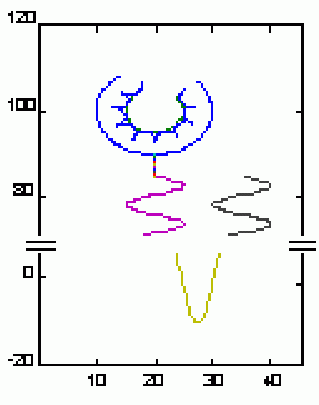
Figure 2

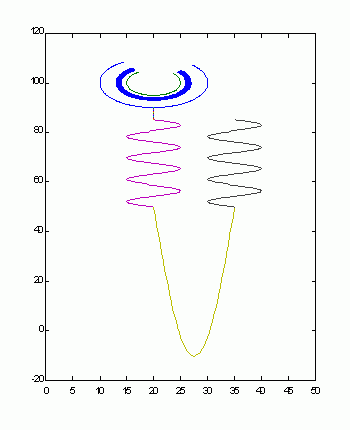
Figure 3

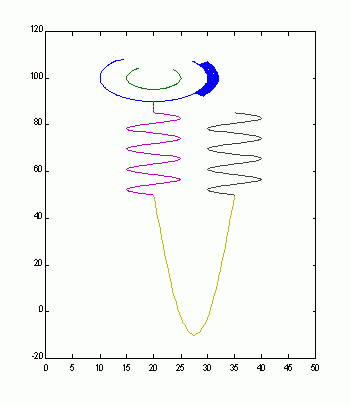
Figure 4

We know that the glomerulus in illnesses states only deforms to a limited scope of morphological options and that this histological patterns are not privative of an illness but that different renal entities meet identical glomerulus patterns. May be, the glomerulus, before the different noxa that attack it, can respond with a limited number of deformities that would not be random but determined by different attractors.

We conclude that from the fractal geometry, the sinusoidal function could explain not only the normal nephrological structure but also that of the glomerular histopathological patterns.

REFERENCES

Prigogine I. Las leyes del caos. Barcelona. Crítica. 1997
Hayles K. La evolución del caos. Barcelona. Gedisa. 1993
Lipsitz L, Goldberger A. Loss of complexity and aging. JAMA 1992; 267: 1806-1809
Goldberger A. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. The Lancet 1996; 347: 1312-1314
Editorials. Fractals and medicine. The Lancet 1991; 338: 1425-1426
Lewin R. Complejidad. Barcelona. Metatemas: 1995
Landsberg PT, Ludwig G, TOM R, Schatzman E, Margalef R, Prigogine I. Proceso al azar. Barcelona. Metatemas.1992
Elbert T, Ray W, Kowalik Z, Skinner J, Graf KE, Birbauer N. Chaos and physiology: Deterministic chaos in excitable cell assemblies. Physiological Reviews. 1994; 74: 1-41
Chaos Williams GP. Chaos Theory Tamed. Joseph Henry Press, Washington, 1997.
Sussman GJ, Wisdom J, Mayer ME. Structure and Interpretation of Classical Mechanics. The MIT Press, Cambridge, Massachusetts. 2000.
Gollub JP. Order and disorder in fluid motion. Proc. Natl Acad Sci, Vol 92, pp 6705-6711, July 1995.
Mallat S. A Wavelet Tour of signal processing. Academic Press, 1998.
Falconer K. Fractal Geometry: mathematical foundations and applications. John Wiley and sons, 1990.
Murray JD. Use and abuse of fractals, in Mathematical biology. Springer, 2002
Semmlow JL. Biosignal and Biomedical Image Processing, MATLAB Based Applications. Marcel Dekker, New York – Basel. 2004.
Rosenblatt J, Stoughton B. Mathematical Analysis for Modeling. CRC Press.1999.
Yip K, Holstein-Rathlou N. Chaos and non-linear phenomena in renal vascular control. Cardiovascular Research 1996; 31: 359-370
Yip KP, Holstein-Rathlou NH, Marsh DJ. Chaos in blood flow control in genetic and renovascular hypertensive rats. Am. J. Physiol.261 (Renal Fluid Electrolyte Physiol.30): F400-F408, 1991.

Comment of the reviewer Prof. Jose Luis Hernandez Caceres, PhD. Center for Cybernetics Applications to Medicine (CECAM), La Habana. Cuba

Fractal geometry is based on the idea of a repetitive pattern acting at different spatial scales. In this context, the idea of a repetitive sinusoidal pattern is not trivial. However, the morphology of both the normal and diseased nephron seems to be adequately correlated with this type of fractals. Moreover, the authors have found that some pathological states are rather associated with a reduction in the diversity of possible sinusoidal configurations.

The fact that this ideas are supported by observation, plus the possibility to quantitatively assess the pathological conditions, make this work worth of attention. A further step could be to find the sets of parameter/states associated with individual pathologies.

Comment of the reviewer Prof. Fernando Tricas PhD. Facultad de Informática. University of Zaragoza. Zaragoza. España

'Strange attractors appear when representing the phase space of dynamical systems's evolution.
They are charecterized for its fractal dimension and they represent a probability cloud which will be more dense in the zone more frequently visited.
These kind of systems appear frequently in natural systems and, in this sense, it is interesting to try to evaluate if some cellular structures can follow this kind of dynamics.

Received: August 23, 2006. Received reviewed: December 15, 2006
Published: January 26, 2007

MEDICAL HYPOTHESES

HISTOLOGICAL GLOMERULAR PATTERNS AS CHAOTIC ATTRACTORS

Musso C¹, Bezic J¹, Christiansen S³, Algranati L¹

¹Servicios de Nefrologia y ³Anatomía Patológica. Hospital Italiano de Buenos Aires.
National University of Entre Rios, Engineering School². Argentina

carlos.musso @ hospitalitaliano.org.ar

Rev Electron Biomed / Electron J Biomed 2007;1:21-27