Indice del volumen Volume index
Comité Editorial Editorial Board
Comité Científico Scientific Committee
- Order of the autoregressive model (r). It reflects the number of past values necessary to optimally describe the autoregressive function.
- Nonlinear correlation coefficient expressed as:
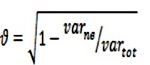
where Vtot corresponds to the signal's variance and Vne is the unexplained variance after applying the model. In the linear case, this expression is equivalent to the linear correlation coefficient 14.
LOW DIMENSIONAL ATTRACTORS AMONG PERIPHERAL PHOTOPLETHYSMOGRAPHIC SIGNALS: RELATIVE PROPORTION AND CHANGES WITH AGE.
Javier Jas*, Jose Luis Hernandez Caceres**, Ismelis Iglesias***.
* Instituto Superior de Cultura Fisica "Manuel Fajardo".
** CECAM. *** Centro Nacional de Bioinformática
La Habana. Cuba.
julian.garcia @ infomed.sld.cu
Rev Electron Biomed / Electron J Biomed 2010;2:33-40.
Comment of the reviewer reviewer D. Eduardo Tejera Puente. Doctorando en Universidad de Oporto. Portugal.
Comment of the reviewer reviewer Luis Garcia Dominguez PhD. Hospital for Sick Children. Toronto. Canada
ABSTRACT
Previous studies showed that the finger Photoplethysmographic (PPG) signal contains several dynamically distinct components. This work is focused on the characterization of the low-dimensional nonlinear component of the PPG signal.
Nine young (5-22 years of age) and ten adult (30-91 y) presumptively healthy subjects were recorded during 10 minutes in supine position. Each individual traces was divided into non-overlapping segments each with 500 data points, and kernel nonlinear estimation was performed. Noise free Realizations (NFR) were generated for each nonlinearly estimated segment.
We obtained that 72.8% (657 out of 902 analyzed NFR) of the NFR were periodic, corresponding to limit cycle attractors. Besides, 14.4% of the attractors were chaotic, and 7.4% of the NFR corresponded to point attractors. In 47 NFR (5.2%) the appearance was either periodic or chaotic, but their amplitude was less than 10% of the original trace. We classified these traces as 'quasi-punctual'. Thus, besides previously described periodic attractors, chaotic, quasi-punctual and point attractors may be found. Proportions for each type of attractors varied among subjects, and periodic attractors were more abundant among older subjects (p<0.05).
We interpret these results as an evidence of maturation of the nonlinear cardiovascular dynamics. We stress that the contribution of stochastic influences into the PPG signal cannot be omitted. Limit cycle dynamics apparently warranties a better robustness of the system. Since PPG's stochastic component is a fractal motion, the study of the interaction between this fractal component and the low-dimensional nonlinear system need to be theoretically handled to understand their implications for cardiovascular physiology.
KEYWORDS: Photoplethysmographic signal. Nonlinear dynamics. Chaos.
RESUMEN
Estudios anteriores mostraron que la señal fotopletismográfica contiene varios componentes distinguibles desde el punto de vista dinámico. El presente trabajo se ha centrado en la caracterización del componente de baja dimensión, de esa señal.
Nueve sujetos jóvenes (5-22 años de edad) y 10 adultos (30-91 años) todos presuntamente sanos, fueron registrados durante diez minutos en posición supina. Cada registro individual fue subdividido en segmentos de 500 puntos cada uno, y cada segmento fue analizado mediante una metodología de análisis autoregresivo no lineal. A partir de la función autoregresiva estimada para cada segmento se generó la realización libre de ruido (RLR) correspondiente.
Se obtuvo que el 72.8% (657 de las 902 RLR analizadas) de las RLR fueron periódicas, correspondientes a tractores de tipo ciclo límite. Por otra parte, el 14.4% de los atractores eran caóticos mientras que hubo un 7.4% de atractores puntales. En 47 segmentos (5.2%) la apariencia de las RLR era periódica o caótica, pero con del 10% de la amplitud del correspondiente trazo original, y fueron clasificadas como "casipuntuales". De esta manera, además de los atractores periódicos reportados con anterioridad, es posible encontrar atractores caóticos, puntuales y casipuntuales. Las proporciones de cada tipo de atractor variaba de un individuo a otro, siendo los atractores periódicos más abundantes entre los adultos (p<0.05).
Estos resultados son interpretados como una evidencia de la maduración de la dinámica cardiovascular. Se destaca que la contribución de las influencias estocásticas a la generación de la señal fotopletismográfica no debe ignorarse. La dinámica de tipo ciclo límite al parecer garantiza una mejor robustez el sistema. Al ser el componente fractal de la señal fractal, estudio de la interacción de este componente fractal y el sistema no lineal debe tratarse teóricamente para una mejor comprensión de sus implicaciones para a fisiología cardiovascular.
PALABRAS CLAVE: Señal fotopletismográfica. Dinámica no lineal. Caos.
INTRODUCTION
The waveform of the finger photoplethysmographic (PPG) signal has been used as a valuable source of information about vessels' compliance and their modification with condition, drug, and presence of pathology1-2.
The photoplethysmographic signal provides a continuous recording of changes in the volume of blood vessels bathing a limb (in our case a finger) at each heart stroke. The pulse wave has a peculiar shape, and parameters derived from its morphology have been used for measuring the degree of vessels' stiffness3-4.
From the simultaneous measurement of PPG signals from different sites of a subject's body the transit time of the mechanical pulse wave can be measured, and information about pulse wave velocity can be obtained5. Pulse wave velocity depends mainly upon mechanical properties of both vessels and blood, as well as on the arterial tree configuration. Even when theoretical models for realistic situations are incomplete, it seems plausible to expect that autonomic nervous system modulation of the blood vessels might also modulate pulse wave velocity.
Added to the widely documented fact that the variability of the interval between successive wave peaks is closely related to the variability of heart rate it is to expect that some aspects of the complex dynamics of autonomous nerve system activity at the global level is being reflected in the PPG signal6.
Much theoretical effort is being devoted to understanding the shape of a single PPG wave, where the original pulse wave raveling from the heart to the finger is added to at least one reflected wave coming apparently from lower parts of the body3. Our preliminary results about the shape of the waveform suggest that the shape of the waveform changes from pulse to pulse, ans this variability is more prominent in the final part of the wave, that apparently correspond to the contribution of reflected wave(s).
It seems plausible to assume that besides the approach focused on the morphology of individual waveforms7-8, the PPG signal can be viewed as emerging from a complex system were tools from nonlinear science can be appropriate, as it has been suggested for other cardiovascular signals29. The possibility of de-composing the PPG signal into different contributing elements has been suggested by different studies9-10. In particular it seems possible to estimate the nonlinear dynamics of PPG stationary component through a nonlinear identification approach11-12. We hypothesize that an approach based on nonlinear identification and complexity theory can be useful for the study of this particularly revealing signal. This line of thought brought Hernandez et al to the identification of the fractal component of the PPG signal, and preliminary evidences about their modification in pregnancy were suggested13-14. Another component is the low-dimensional attractor. According to the first reports using a nonlinear identification approach, the low-dimensional attractor is a limit cycle, whose periodic noise free realizations mimic the morphology of the original waveform.
This report has been focused on the characterization of the low-dimensional nonlinear component of the PPG signal taken from a larger data set. Results from current research refine previous conclusions. In particular, we report that although most of the segments presented periodic NFR, also punctual, quasi-punctual and chaotic attractors are present. Apparently, the proportion of attractors varies with age, suggesting that our approach can provide further insights into cardiovascular system maturation in humans.
MATERIALS AND METHODS
Sixteen presumably healthy subjects (05 -91 years) participated in the study. All of them were informed of the characteristics of the test and accepted to take part of it. Children's parents were asked and accepted their involvement in the study. Ten minutes in supine position of PPG waveform data was digitized with a sampling rate of 75 Hz (pulse oxymeter Oxy 9800, Combiomeq). PPG signal was recorded from the left pointer finger, and the hand was laid on the bed, at the side of the body. Pulse oxymeter sends continuously the digitized signal to the serial port of a PC where it is collected and stored. All the statistical processing was performed off-line.
Baseline of each recorded PPG signal was corrected by subtracting a 22-order whole signal adjusted polynomial of the type:
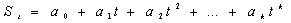
Where St is the photoplethysmographic signal evaluated at time t; a0,a1,…,ak, are real constants, corresponding to the model's coefficients.
Trend-corrected signals were divided in approximately 55 segments of 500 data points to reduce the non-stationarity of the signal. Nonlinear dynamics identification and a noise free realization were estimated to each segment.
Nonlinear Dynamics identification. Kernel nonparametric analysis was applied to each segment of trend-corrected signal. In kernel autoregression, the segment is fitted to a model of the type:
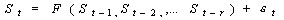
The function nonlinear F is obtained as a weighted average of the observed points in the phase space, the nearest points bearing the highest contribution. For more details about the method, see references1, 13-14.
During the application of the kernel procedure, the following information was obtained:
A Matlab/Scilab version of the program used is freely available from authors upon request.
Noise free realization generation (NFR). The noise free realization was obtained via sequential estimation of the function F to previously estimated data points of the time series. The initial points of the series are set at random. The 100 first points of the NFR are discarded for assuring the absence of transients in the NFR.
The phase portrait reconstructed from the NFR gives information about the noise free dynamical system. Either time domain NFR or corresponding phase portraits are provided for illustrating the types of attractors obtained.
RESULTS
A total of 902 segments were obtained from the 16 individual recordings. Each segment contained 500 data points. Nonlinear identification was applied to each segment. From each segment a noise free realization was estimated.
The following types of NFR were found.
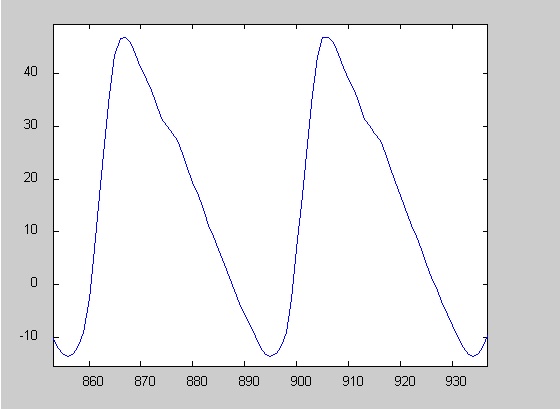
Figure 1 Segment from a periodic NFR.
Periodic NFR. A total of 657 (72.8% of total) periodic NFR were found. Typically, they resembled both in shape and amplitude the waveform of the original PPG signal.
As apparent from figure 1, details from the original waveform are recovered in the NFR, including the bulging associated to the presence of reflected waves.
Chaotic NFR. A total of 130 (14.4%) chaotic NFR were observed. As a rule, the shape of chaotic NFR resembles both the amplitude and the shape of the original tracing, though some of them were quite bizarre. Phase plots of some chaotic NFR are shown in figures 2 and 3.
Point Attractors. In 67 segments (7.4% of the total) the NFR resembled the trajectory of a damped pendulum, converging to a flat trace, corresponding to a point attractor.
Quasi-punctual NFR. In 47 NFR (5.2%) the appearance was either periodic or chaotic, but their amplitude was less than 10% of the original trace. We classify these traces as 'quasi-punctual'.
Relationship between the type of attractor and individual condition. The distribution of attractors varied widely between recorded subjects; thus periodic attractors ranged from 38.9% to 98.4% among the recorded subjects. For chaotic attractors, individual percentages varied between zero and 39.6%. Point attractors ranged between zero and 34.7%. For quasi-punctual attractors, percentages varied from zero to 16.7%.
We could not find significant regression of any value respect to age, perhaps due to the small size of the data. As an alternative to check changes associated to age, the sample was divided into two groups, one with 9 subjects aged between 5 and 22 years, and the other between 30 and 91 years of age (7 individuals).
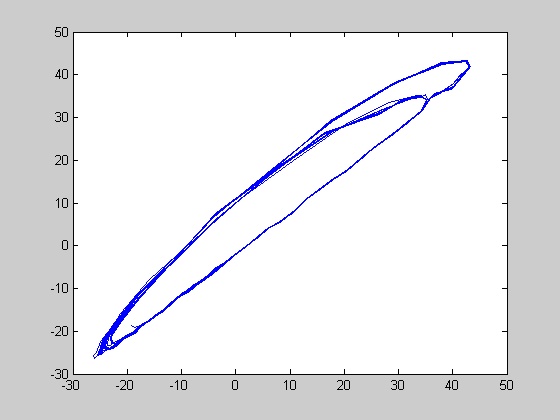
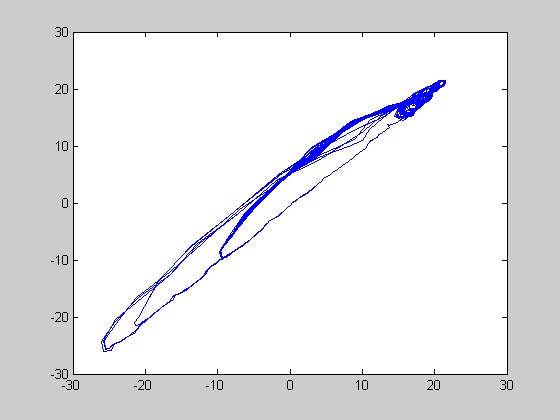
Figures 2 and 3 phase plots of two different chaotic NFR
We found that the elder subjects had a higher abundance of periodic attractors (78.5 vs 69.6%; p= 0.0017). A mirrored proportion was observed for point attractors (4.6% among older vs. 9 % among younger subjects; p=0.015).
No significant differences were observed among both groups for chaotic or quasi-periodic attractors.
DISCUSSION
Studying a larger data set, we refined a previous report about limit cycle low dimensional attractors in PPG signals13. Even when they are the most abundant, more than a quarter of the NFR are either punctual or chaotic. Apparently, the abundance of punctual attractors is higher among younger individuals.
From the viewpoint of nonlinear science, this result, added upon the previously reported fractal nature of non-deterministic components of the PPG signal13, might be of interest.
A further step can be trying to understand these results on the light of available knowledge about cardiovascular physiology.
Noise, stochastic contribution, etc, is a mathematical concept. To pretend to identify a real physiological process with noise is not theoretically founded forehand. At the same time, it seems that the autonomic activity, due to its smaller time scale and due to its vibration-like appearance, is a good candidate for representing the fractal noise that has been described in the PG signal.
If one accepts that the "noise" corresponds to the autonomic regulation, our results can be associated to certain implications.
In nonlinear dynamics, "noise" is not a mere disturbance masking real processes, as it could be with a TV signal recorded in a poor-reception area. Here stochastic contributions are regarded as innovation noise feeding the system, as the case of a training bag for boxing, whose inner dynamics is that of a point attractor. The (randomly delivered) blows of the athlete heep the bag swinging. From our methodology perspective, the NFR of the bag is a point attractor, and the observed oscillations are result of the random blows, that are, in this case, separated from the deterministic component.
Seen from this perspective, point attractors in PPG signals might reflect a state when the almost periodic behaviour of the observed signals is a consequence of the innovation noise, in this case of the influence of the ANS. The presence of point attractors can be the result of a numerical artefact, when the dynamics, for instance, changes and the weighted average reflects the less inconvenient of the possibilities. At the same time, as realizations of linear autoregressive models can show11, a linear dynamics fed by stochastic input can mimetize the appearance of waveforms. We are more prone to accept this last possibility, on first instance because stochastic components are apparently there and also because visual inspection of the corresponding segments is not suggesting abrupt changes in dynamics.
Periodic attractors could reflect a state when the inner dynamics of the system, is so coupled that a periodic behaviour is possible even when ANS input is absent. From this viewpoint, periodic NFR might reflect a more robust respect to perturbations dynamics. The fact that this type of attractos is more abundant among adults might be a reflection of maturation of the blood delivering mechanisms.
Reported evidence on heart rhythm dynamics among heart transplanted individuals could serve as guidance for our results.
A transplanted heart, during the first 10 days after surgery, is devoid of nervous regulatory mechanisms, and the heart shows "metronome-like" chronotropic behaviour15. The intrinsic pacemaker dynamic leads heart's activity. The prominent presence of limit cycle in our results might point to a dynamics of self sustained oscillations, with all the variability supported by extrinsic stochastic-fractal process. That could be explained by this pacemaker alone based regulation.
The fact that the limit cycle corresponds to low dimensionality (no more than 2 previous values are required in the autoregressive model) is noticeworth. The PPG signal reflects not only heart contractions, but also the transfer of the pulse wave through a putatively fractal network of vessel whose response to haemodynamic stimuli may be extremely complex (16-18). The fact that this system exhibits a low-dimensional periodic dynamics might reflect not a degradation, but a very shroud degree of coupling where the basic function is warranted with minimal external regulation. The ANS will modify the intrinsic dynamics only upon body's request.
Following limit cycle, chaotic attractors are the second most abundant type of dynamics observed. This leads to the idea of intrinsic chaos in the PPG signal generation. Variability in the frequency of the signal is related to HRV and amplitude variations depend primarily of central blood pressure and constriction of the arterioles19. Respiratory depth and frequency also affect indirectly amplitude and frequency of the signal20. All of these elements contain very rich dynamic motions.
Presence of chaos in the heart rate is a controversial topic21-22. But is a fact that in the period from 11-100 days the transplanted heart starts an improvement of the rhythm's intrinsic complexity, even without any external autonomous inputs 15. The heart adapts to the new environment and develops its own means for self-regulation. This idea of nonlinear behaviour of heart rate, non related to the ANS, is supported by several studies23-25. Also variability of heart contractility, reflected in blood pressure variability, shows chaotic behaviour26.
It is accepted that small arteries and arterioles have chaotic changes in diameter that produce either chaos in vascular resistance and in blood pressure27. It has been suggested that this chaotic behaviour has an intrinsic origin but it is regulated by the autonomous nervous system28. Our results show changes in the dynamic from a type of attractor to other and transition from regular to highly aperiodic behaviour is seen in the vascular dynamic. We suspect that the method is sensible to the changes in strategies of the cardiovascular system.
In this sense, the study of PPG signal non-linear dynamics might open new possibility for the study of CV system as well as possible modification with disease.
Thus our results suggest that there is a sort of maturation in the nonlinear dynamics of the individual with age. A higher abundance of periodic attractors might reflect a higher robustness of the CV system. To explore concrete details of this maturation process is a major goal from our group.
ACKNOWLEDGEMENTS: Authors would like to thank Professors Alicia Juarrero and Christopher Cherniak for their comments about our work when this research was on an earlier stage. The comments from two unknown referees enriched our views on this topic.
REFERENCES
-
1.- Allen J. Photoplethysmography and its application in clinical physiological measurement. Physiol Meas. 2007; 28 R1-R39.
2.- Shelley K. Photoplethysmography: Beyond the Calculation of Arterial Oxygen Saturation and Heart Rate. Anesth Analg 2007; 105:S31-6.
3.- Millasseau, et al. Contour analysis of the photoplethysmographic pulse measured at the finger. J Hypertens 2006; 24:1449-1456.
4.- Guerrisi M. et al. Differential response of peripheral arterial compliance-related indices to a vasoconstrictive stimulus. Physiol. Meas. 2009; 30:81-100.
5.- Inoue N et al. Aortic Pulse Wave Velocity Predicts Cardiovascular Mortality in Middle-Aged and Elderly Japanese Men Circ J. 2009;73: 549 - 553
6.- Sheng Lu. et al. Can photoplethysmography variability serve as an alternative approach to obtain heart rate variability information? J. Clin Mon. 2008; 22:23-29
7.- Monné Y. et al, Study of pulse wave morphology and cardiovascular level risk relationship applying non-supervised classification. VII Cong Int Inf Sal 2009: SLD083.
8.- Otsuka T. et al, Independent Determinants of Second Derivative of the Finger Photoplethysmogram among Various Cardiovascular Risk Factors in Middle-Aged Men. Hypertens Res 2007; 30: 1211-1218
9.- Hong R. et al. Analysis of the photoplethysmographic signal by means of the decomposition in principal components. Physiol. Meas. 2002;23 N17
10.- Bhattacharya J. et al. Analysis and characterization of photo-plethysmographic signal. IEEE Trans Biomed Eng. 2001;48:5-11.
11.- Haerdle W, et al. A review of nonparametric time series analysis Int Stat Rev. 1997; 65: 49-72
12.- Small M. Estimating the distribution of dynamic invariants: illustrated with an application to human photo-plethysmographic time series. Nonlinear Biomed Phys. 2007;1:8
13.- Hernández J. L. et al. The Photoplethismographic Signal Processed with Nonlinear Time Series Analysis Tools. Rev Cub Inform Med. 2001;1:1-10.
14.- Cabañas K et al, Evidence of variation in the fractal component of the plethysmographic signal under different physiological conditions. Mem. Informática 2000, La Habana.
15.- J. Yasha Kresh and Igor Izrailtyan Evolution in functional complexity of heart rate dynamics: a measure of cardiac allograft adaptability. Am J Physiol Regul Integr Comp Physiol. 1998; 275: R720-R727.
16.- Alastruey J. et al. Analysing the pattern of pulse waves in arterial networks: a time-domain study. J Eng Math 2009;64:331-351.
17.- Cohen M. and J. Andrew Taylor Short-term cardiovascular oscillations in man: measuring and modelling the physiologies. J. Physiol 2002;542:669-6838.
18.- Wagner CD. et al. Chaos in blood pressure control. Cardiovascular Research 1996;31:380-387
19.- Jong Y. A. Foo, et al. Photoplethysmographic Assessment of Hemodynamic Variations Using Pulsatile Tissue Blood Volume. Angiology 2009;59:745-752.
20.- Selvaraj N. Influence of respiratory rate on the variability of blood volume pulse characteristics. J Med Eng Technol 2009;33: 370-375.
21.- Zhang, JQ et al. Stochastic vagal modulation of cardiac pacemaking may lead to erroneous identification of cardiac "chaos". Chaos 2009;19:028509
22.- Baillie R et al. Normal heartbeat series are nonchaotic, nonlinear, and multifractal: New evidence from semiparametric and parametric tests. Chaos 2009;19: 028503
23.- Guzzetti S, et al. Non-linear dynamics and chaotic indices in heart rate variability of normal subjects and heart-transplanted patients. Cardiovasc Res. 1996;31:441-446.
24.- Beckers F. et al. Effects of autonomic blockade on non-linear cardiovascular variability indices in rats. Clin Exp Pharmacol Physiol 2006;33:431-439.
25.- Hagerman I. et al. Chaos-related deterministic regulation of heart rate variability in time- and frequency domains: effects of autonomic blockade and exercise. Cardiovasc Res 1996;31: 410-418.
26 Wagner CD. et al. Chaos in blood pressure control. Cardiovascular Research. 1996;31 : 380-387
27.- Stergiopulos N. et al. Arterial vasomotion: effect of flow and evidence of nonlinear dynamics. Am. J Physiol 1998;274: H1858-64.
28.- Wagner CD. et al Complexity and "chaos" in blood pressure after baroreceptor denervation of conscious dogs. Am J Physiol. 1995;269: H1760-6.
29.- Sharma V. Deterministic Chaos and Fractal Complexity in the Dynamics of Cardiovascular Behavior: Perspectives on a New Frontier. Open Cardiovasc Med J. 2009;3: 110-123
Correspondence:
Email: julian.garcia @ infomed.sld.cu
