ISSN: 1697-090X

Inicio Home

Indice del volumen Volume index

Comité Editorial Editorial Board

Comité Científico Scientific Committee

Normas para los autores Instruction to Authors


Derechos de autor Copyright

Contacto/Contact:


    Letters to the Editor / Cartas al Editor


    AN ATTEMPT OF EARLY PREDICTION AND LATER ASSESSMENT OF THE CHOLERA OUTBREAK
    IN HAITI (OCTOBER 2010).

    Jose Luis Hernandez Caceres1, Berhanu Dibaba Kumma2, Graham Wright3

    1 Center for Cybernetics Applications to Medicine.
    Havana Medical University. Cuba
    2 Embassy of the Federal Democratic Republic of Ethiopia in Havana, Cuba
    3Walter Sisulu University, Eastern Cape, South Africa


    cacerjlh @ infomed.sld.cu


    Rev Electron Biomed / Electron J Biomed 2011;1:87-90.



    To the Editor:

    Regretfully, epidemics are becoming a more usual than desired phenomenon. AIDS, Ebola, SARS, H1N1, Avian flu, are words not known to our grandparents.

    Haiti, the poorest country of the western hemisphere, immersed in the process recovering from an earthquake that killed more than 200 000 citizens and subsequently hit by a hurricane, is facing, since October 2010, an epidemic of cholera, a disease that was absent in that country for decades.

    To predict the fate of an outbreak is useful for health care providers, especially when optimal resource management is crucial. However, outbreak prediction is not a theoretically granted undertaking. Nevertheless, there are few attempts in that direction.

    In the case of the Haitian outbreak, an early estimate by UN Office for the Coordination of Humanitarian Affairs projected 200.000 cases, based in the rather simplistic assumption that all of the population is at risk of contracting cholera, and estimating a cholera attack rate of 2%.1

    On December 30th 2010, the government of Haiti operatively expected 500.000 cases for 1 year, half of them during the first three months 2.

    On March 16th, 2011, Andrews and Basu published in "The Lancet" a detailed mathematical model for the Haitian cholera outbreak. Their analysis suggests almost 800.000 cases of cholera between March 1 and Nov 30, 20113.

    We used a version of the methodology proposed by Hernandez Caceres for outbreak prediction4-5. It is based on the assumption that many really occurring epidemics can be nicely described with the Richards's model that was introduced recently by Hsieh et al6-7.

    According to this model, the cumulative number of cases as a function of time (S(t))can be represented as

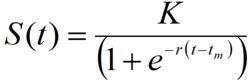
    The three parameters of this model have concrete epidemiological meaning.

    K is the size of the epidemic or the total number of cases; tm is the turning point or moment of maximal incidence, when half of the total number of cases has been accumulated.

    The parameter r refers to the rate of cases accumulation and is related to the basic reproductive number R0 through the expression.

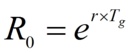
    Where Tg is the so-called generation time, or time between the appearance of symptoms in a primary case and the appearance of symptoms in a secondary case.

    Much can be argued about the flaws of this approach. However, these two statements can be said in favor.

    1.- The Richards's model is compatible with a realistic solution to the seminal model by Kendrick and McCormick8.

    2.- Many real epidemics can be described through it.

    As an illustration, the cumulative cases of cholera during the 2009 outbreak in Zimbabwe can be approximately fairly with Richards's model.



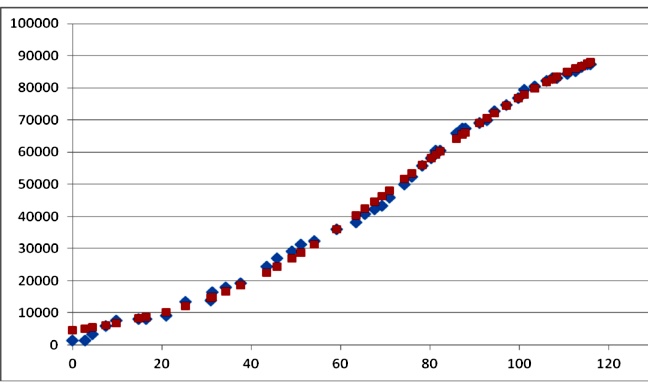
    Figure 1. Cases of cholera in Zimbabwe (rhombs), and fit with Richards's model (squares). The best fit parameters were: K=103979; r=0.041; tm=74.6 days (r2=0.9973). Data redrawn from9


    Parameter prediction can be attempted at a very early stage of the outbreak. The methodology is based on linearizing equation1 with further refinement of the estimates based on plausible assumptions. The method is described in4

    We attempted an early forecast on Nov 8, only 19 days since outbreak onset. This early, preliminary estimate yielded:

    • K: 140.000- 1.700.000 cases, (median of 500.000 cases).
    • r: 0.07-0.08
    • tm: 170-180 days;

    Accordingly, and assuming a generation time of 10 days we obtained R0 =2.72. This value is similar to the value of R0 between 2.06 and 2.78 reported in10.

    The prediction of 500000 cases and the duration (2Xtm) of 1 year is close to the prediction assumed by Haitian authorities 50 days later on December 30th, 2010.

    Since December 17 with a larger number of data points, we applied a Gauss-Newton algorithm for optimal parameter estimation.

    We obtained the following values:

    • K=347.469
    • r=0.03178 (R0=1.37)
    • tm=78.668

    These predictions have remained practically unchanged till the most recently available data of April 10, 2011 (K=308.353; r=0.028, and tm=77.2)

    The difference of these more precise forecasts respect to our early one might be a reflection of using a more appropriate methodology, but also of proper interventions undertaken during the first weeks of the epidemic.

    Thus, we have at least two forecasts, one based on a simple model assuring less than 400.000 cases in a 6 month period (about the end of April)and another based on a sophisticated model predicting 800.000 extra cases till November 2011. Coming months will reveal the likelihood of each of these two statements.

    Sincerely Yours

    Jose Luis Hernandez Caceres,
    Berhanu Dibaba Kumma and
    Graham Wright.



    REFERENCES

      1.- UN Office for the Coordination of Humanitarian Affairs. Cholera Inter-Sector Response Strategy for Haiti: Nov 2010-Dec 2011. 2010, United Nations. New York.

      2.- The UN Health Cluster in Haiti. Cholera continues to spread as response scales up. Haiti health cluster bulletin, 2010. (13). Available at: http://new.paho.org/hq/index.php

      3.- Andrews J. R., and Basu, S., Transmission dynamics and control of cholera in Haiti: an epidemic model. The Lancet 2011. Early Online Publication, 16 March. Available at: http://www.thelancet.com/journals/lancet/article/PIIS0140-6736(11)60273-0/

      4.- Hernández Cáceres JL, Vázquez Argote K, Risco Soria R, Martín Martínez M. Attempting to predict the fate of an ongoing epidemic. Lessons from A (H1N1) influenza in USA. Electron J Biomed 2009;2:38-48

      5.- Hernandez Caceres, J. L.. Attempt to Predict an Ongoing Epidemic Outbreak. The case of A (H1N1) Influenza in USA. In: Safran C. et al., eds. MEDINFO 2010. IOS Press, 447-451. Cape Town. doi:10.3233/978-1-60750-588-4-447

      6.- Hsieh YH. Richards model: a simple procedure for real-time prediction of outbreak severity. In: Ma Z, Wu J, Zhou Y, eds. Modeling and Dynamics of Infectious Diseases. Series in Contemporary Applied Mathematics (CAM). Volume 11, 218-239, 2008. Beijing: Higher Education Press.

      7.- Hsieh YH. Pandemic influenza A (H1N1) during winter influenza season in the southern hemisphere. Influenza and Other Respiratory Viruses, 2010. 4 (4): p. 187-197.

      8.- Kermack, W. O. and McKendrick, A. G. Contributions to the mathematical theory of epidemics. Proc R Soc Lond A. 1927; 115: 700-721.

      9.- World Health Organization. Cholera in Zimbabwe: Epidemiological Bulletin, 2009. (13 ). Available at: http://www.who.int/hac/crises/zwe/sitreps/zimbabwe_weekly_16_22_28march2009.pdf

      10.- Tuite AR, Tien J, Eisenberg M, Earn DJ, Ma J, Fisman DN. Cholera Epidemic in Haiti, 2010: Using a Transmission Model to Explain Spatial Spread of Disease and Identify Optimal Control Interventions. Ann Intern Med. 2011; 154 (7). [Epub ahead of print]


    CORRESPONDENCE:
    Jose Luis Hernandez Caceres MD
    Center for Cybernetics Applications to Medicine.
    Havana Medical University. Cuba
    cacerjlh @ infomed.sld.cu



    Received: January 28, 2011.
    Published: April 16, 2011