Rev Electron Biomed / Electron J Biomed 2006;2:34-45. Hernández Cáceres et al. PRE VACCINATION MEASLES OUTBREAKS ...

Comment of the reviewer Douglas R McLean PhD. Lecturer in Mathematics and Statistics. Department of Computing Science and Mathematics. University of Stirling, Stirling. Scotland. UK.

Comment of the reviewer Prof. Maykel Cruz Monteagudo. Applied Chemistry Research Center, Faculty of Chemical-Pharmacy. Department of Drug Design, Chemical Bioactive Center. Central University of Las Villas. Villa Clara. Cuba

ABSTRACT
Measles data from pre-vaccination era in England and Wales were submitted to nonlinear association analysis. The method's rationale lies on the supposal that strong association between two time series when one of them is shifted in time respect to the other might be taken as an evidence for spatial-temporal causality. A threshold value for the nonlinear determination coefficient (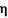) was set as criterion of strong association ( 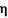> 0.55).

The common pattern for most of the cities was that outbreaks in a given place might be anticipated by some cities whereas followed by others. Only Preston preceded other cities and never followed any other. This result might be plausible since this port is an important node of human exchange with other cities. The associations respect to Preston were markedly nonlinear and the spread from there was slower, perhaps due to climatic causes. We conclude that nonlinear association approach is a promising way of exploring spatial-temporal epidemics data.

Keywords: Epidemics spread, measles, nonlinear association.

RESUMEN:
Se estudiaron, mediante un método de análisis de asociación no lineal, datos de incidencia de sarampión en Inglaterra y Gales correspondientes a la era pre-vacunación. La idea del método se centra en suponer que una asociación fuerte entre dos series temporales cuando una esta desplazada en el eje del tiempo respecto a la otra puede ser tomada como evidencia de causalidad. Se predeterminó un valor umbral para el coeficiente de determinación no lineal (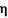) como criterio de asociación fuerte ( 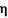> 0.55).

Para la mayor parte de las ciudades los brotes epidémicos se anticipaban a los de otras ciudades, pero eran posteriores a unas terceras. Solamente Preston precedía a otras ciudades y nunca siguió a otra. Este resultado pudiera ser relevante por cuanto este puerto es un nodo importante de intercambio humano con otras ciudades. Las asociaciones respecto a Preston eran marcadamente no lineales y la propagación desde Preston era más lenta, quizás debido al clima. Concluimos que un enfoque de asociación no lineal es una vía prometedora para explorar datos espacio-temporales de epidemias.

Palabras clave: Propagación de epidemias, sarampión, asociación no lineal.

INTRODUCTION

Mounting evidence supports the nonlinear stochastic nature of epidemics dynamics^1-7. Since epidemics involve both space and time, this may imply the presence of bifurcations on one hand, and nonlinear associations on the other⁸. Consequently, both of these properties should be taken into consideration for assessing spatial-temporal features of epidemics. In particular, an adequate framework is required for studying spread mechanisms. The limitations of available approaches for epidemics propagation have been recognized [5].

There are several other examples of naturally occurring phenomena that convey to a nonlinear stochastic dynamics: brain and heart activity, financial data, population dynamics, sunspots, among others^8-9. It seems sound to explore the use of methods with proven reliability in other areas for the study of epidemics data.

In this work, a nonlinear association method has been applied to the study of a well-known measles incidence database from England and Wales covering more than 20 years of the pre-vaccination era. The nonlinear association method was introduced by P. J. Pijn for assessing the spread patterns of epileptic activity in the brain^10-12. In the version applied here slight modifications to the original version were introduced.

Our characterization of the association between different locations in the area allowed the identification of the port of Preston as a forerunner that synchronizes the dynamics of most of the major cities in the studied area.

Supportive of the plausibility of our results are the following facts: 1) The leading location identified is a port, it means, a node of intense exchange of traveling persons. 2) The values of time lags follow a reasonable pattern considering both distance and availability of communication ways. 3) The associations respect to the focus of spread are strongly nonlinear.

Data and analytical methods used.

Data. Measles epidemic data corresponding to fortnight incidence during pre-vaccination era (1944-1966; 598 data points) among 60 cities from England and Wales were downloaded from the site http://www.zoo.cam.ac.uk/. Data corresponding to each city were saved as ASCII files and selected for further analysis. To study was submitted a subset comprising 300 fortnights starting on the 42^nd fortnight, 1947. All possible pairs of cities were submitted to nonlinear association analysis.

Nonlinear association analysis. A detailed description of the original method appeared in^10-13. The purpose of the method is to quantify the association between two time series assuming that the type of association is not necessarily linear. On a second step, the optimal association is found after shifting signals in time. This allows obtaining an estimate of the time delay between signals. Based on the irreversibility property of physical time, conjectures about causability may be drawn from this analysis. Below, a brief description is summarized.

Let's assume that if the value of a time series Y may be regarded as a function of the value of another time series X, then, the value of Y given X can be predicted according to an estimated regression curve. Since no forehand information about the type of dependence is available, the curve fit must be done in a very wide context. In the original method Pijn used a set of straight segments as an approximation for a nonlinear function^9-12. In a unpublished version used by Pascual-Marqui et al in 1992 [14], kernel nonparametric autorregression was used. Here we approximate the nonlinear dependence with a 3^rd degree polynomial. The variance of Y according to the predicted fit is called "explained" variance due to the knowledge of X. The unexplained variance is estimated by subtracting the explained variance from the original one. The nonlinear association ? describes the reduction of variance of Y that can be obtained by predicting the Y values from those of X according to the regression curve as:
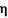= Sqrt((total variance - unexplained variance)/total variance).

It can be shown [9] that in he linear case 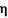is identical to the linear correlation coefficient. For estimation of 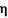we found out the best fit assuming that Y is approximated with a 3rd degree polynomial of X. The order of the polynomial=3 was selected after checking that for third order approximation all the estimated coefficients remained statistically different from zero (p < 0.05).

The nonlinear association index 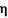ranges from 0 to 1, since only positive roots are considered. We, considered only the case of "strong" association. We consider an association as "strong" if 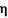> 0.55. This condition warranties a Bonferroni-corrected criterion below 0.01 for the data lengths analyzed.

From the index 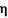, it is also possible to estimate the delay in the coupling between the time series. For this purpose, original data are shifted in time respect to each other, and 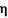is calculated as a function the time delay 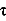. The delay at which the maximum value for 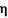is obtained is an estimate of the time lag between the signals. In the case when X causes Y, 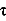y|x will be positive and 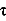x|y will be negative.

RESULTS.

Southampton. In figure 1a data corresponding to Southampton and Plymouth are displayed in one graph. Visual inspection might suggest that measles outbreaks in Plymouth are appearing after outbreaks at Southampton.

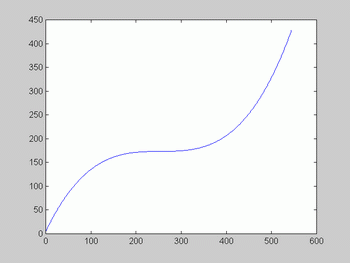
Figure 1a. Measles incidence in Southampton and Plymouth
since 1947 (fortnight 42^nd) until 1959 (fortnight 18^th).

This may be better appreciated in figure 1b, where a particular peak from figure 1a is shown with larger detail.

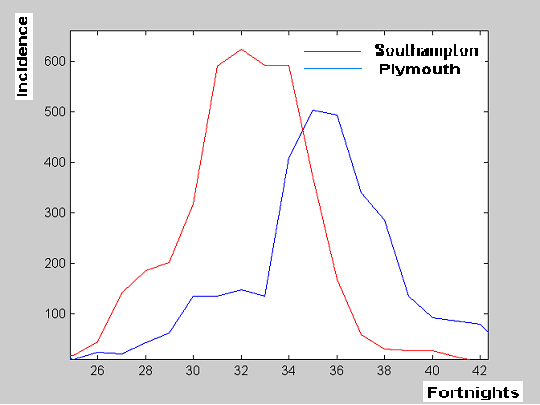
Figure 1b. Excerpt from data in figure 1a.

What is apparent from visual inspection may be confirmed with nonlinear association analysis (Fig 1c): Maximal association is achieved when data from Plymouth are shifted 2 fortnights forwards. Thus the analysis carried out confirmed that measles outbreaks at Southampton precede those from Plymouth.

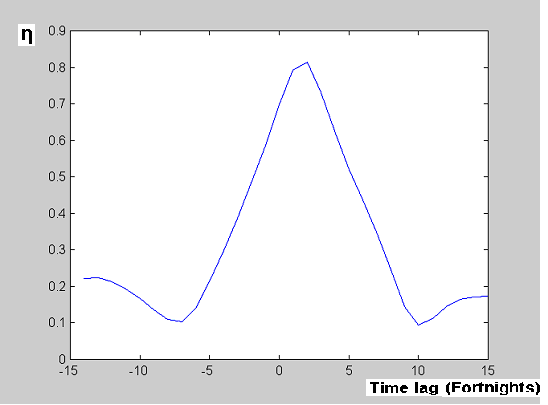
Figure 1c. Nonlinear association analysis for comparison between Southampton and Plymouth.
Optimal association is obtained when Plymouth is lagged two fortnights respect to Southampton.

However, Southampton was not always a forerunner. Our analysis showed, for example, that outbreaks at Southampton go behind those at York following a strong association of =0.7. As apparent from Figure 2a measles outbreaks at Southampton might be preceded by those in Preston.

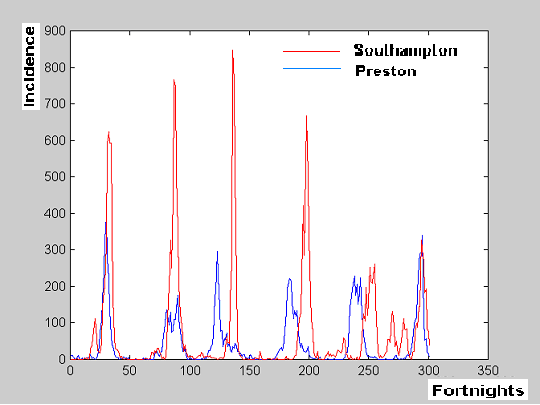
Figure 2a. Data from Southampton and Preston. Legend: see figure 1a.

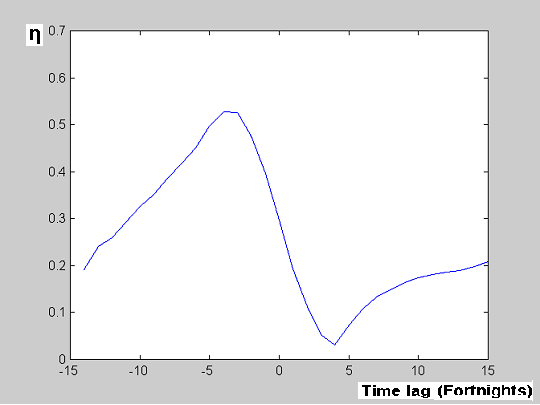
Figure 2b. Nonlinear association between Southampton and Preston.
No support for a strong association is provided.

Nonlinear association analysis suggests a lag of 5 fortnights between both places (fig 2b). However, the maximal association value obtained though significant, was below the threshold of 0.55 and was not regarded as "strong".

Preston. Unlike Southampton, Preston was a "pure" forerunner; its association with other places was markedly nonlinear and the spread from it was slow. After comparing all possible association values in the data matrix, it was obtained that Preston outbreaks never were anticipated by any other location. In table I strong associations for Preston are shown.

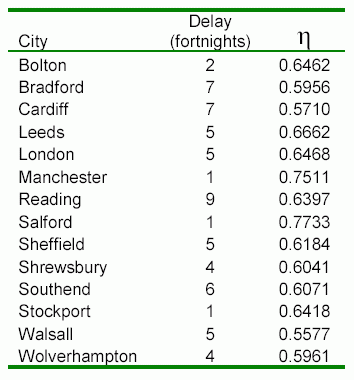
Table I. Strong associations of cities following Preston.

In figure 3, strong associations corresponding to Preston are represented on a map of England and Wales. Data corresponding to Southampton are also included for the case when this port played a leading role.

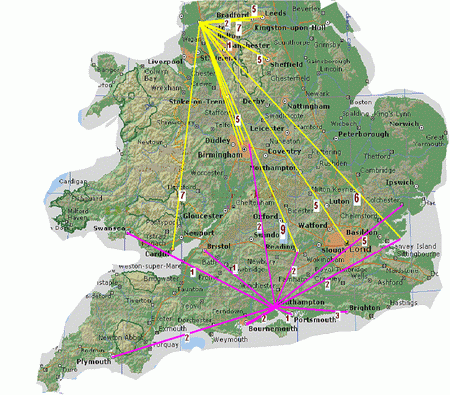
Figure 3. Geographic representation of strong associations with both Preston and Southampton.
Time lags are shown aside of corresponding arrows.

As obtained, with the exception of Liverpool, all major cities of England and Wales are engaged in this scheme.

Spread patterns.

Lag dependence on distance.
As a rule, delays of other cities respect to Preston are increasing with distance. Thus Bolton is 2 fortnights behind, whereas Southen is showing a lag of 6 fortnights. An exception to the common lot may be Bradford, which is much closer than Cardiff, but appears with the same delay. Probably, taking into consideration the frequency of use of corresponding routes could better explain why major cities and important tourist resorts exhibit relatively shorter lags.

Type of Association function.
Fig 4 shows the curve fitted for Salford's dependence respect to Preston at optimal lag.

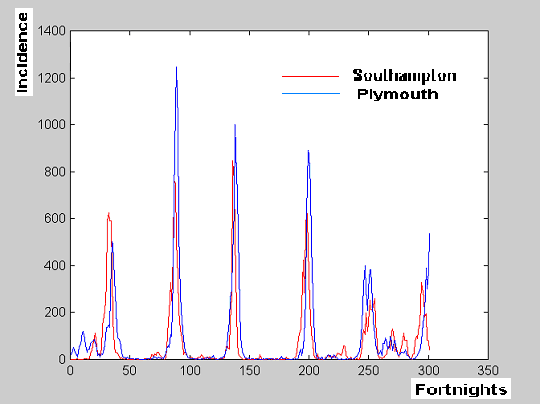
Figure 4. Nonlinear fit explaining Salford as a Function of Preston. Delay=1 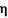=0.77.
Order=3 all regression's coefficients are statistically significant (p < 0.05).

The strong nonlinear appearance of the curve was common for all cities with strong association respect to Preston.

Comparison to Southampton
"Spread velocities" estimated from considering distances and time delays suggest that spread from Preston was apparently more rapid. We found that mean "velocity" for propagation from Preston was nearly twice as large as that from Southampton.

On the other hand, association functions corresponding to Southampton were closer to linearity (fig 5).

Figure 5. Association between Southampton and Plymouth. Delay =2 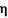=0.81
Compare to figure 4.

DISCUSSION:

Our results with nonlinear association analysis revealed that Preston measles outbreaks were preceding several major cities in England and Wales during 1950's.

It is a common situation for any area involved in data analysis that obtained results are strongly dependent on the chosen method. Accordingly, to avoid method-related bias is a major task. Extreme caution must be taken while trying to extract conclusions on the basis of the results obtained using a particular method.

At this stage of our research, instead of making conclusions about measles spread and putative ways to curtail it, we prefer to concentrate on the soundness of obtained results. Below, we are trying to consider the reliability of both the method and the obtained results.

The method. A common drawback in application of mathematical modelling to real data is the presence of a high number of assumptions whose trustworthiness is difficult to assess. The main virtue of the nonlinear association analysis is its soft attitude regarding assumptions¹³.The restrictions here are reduced to the assumption that a component of a signal may be due to functional dependence respect to another signal. The function is supposed to be smooth and not dependent upon time. Based on the irreversibility of time one may hope that if a signal is partially depending on another signal that preceded it, we may somehow speak about causability. A common situation with real data is their nonstationary nature. In a previous paper with measles data we found that with the data lengths used in this study to assume (quasi)stationarity seems to be justified⁷. On the other hand, to approximate a function with a 3rd degree polynomial is justified from both genera grounds and statistical analysis as well.

At this stage, there are no major reasons to find crucial differences between epidemics data and EEG signals that could disable the nonlinear association method to be applied to our data.

The results. According to our results, Preston was on the lead of measles outbreaks at several major cities in England and Wales (Leeds, Birmingham, London, Southen-on-Sea, Cardiff, Manchester).Other places, as in the case of Southampton, exhibit a significant, but not "strong" dependence on Preston.

Preston is not a Major city in England (about (1/65)th of London's population). However, it is one of the main ports and trade centers of England. Considering the importance of sea transport in an insular country, it is obvious that it is an important node of human exchange in England.

Similarly, Southampton is the most important port in England's southern coast. This might explain the leading role of this place for the synchronization of epidemic waves. Unlike Preston, association with Southampton are closer to linearity, whereas spread id faster.

A possible explanation for a faster spread at Southampton might be related to climatic factors (Preston, located northwest of Southampton is cooler and dryer). It has been suggested that temperature may be operating as an external input modulating measles dynamics^15-16.

Finally, we have not at this stage a reasonable explanation for the differences in the degrees of linearity between Preston and Southampton. Curiously, in epilepsy data nonlinearity becomes stronger when the focus is well established, and not since the beginning^{10, 13}.

Thus we conclude that the nonlinear association approach provides a reliable framework for considering epidemics spread in a geographically distributed area.

Acknowledgements. This paper is dedicated to the memory of the deceased Dr J. P. Pijn, a deep thinker and an excellent man.

REFERENCES

2. Sugihara G, Grenfell B, May RM. Distinguishing error from chaos in ecological time series Philos Trans R Soc Lond B Biol Sci. 1990 Nov 29; 330(1257):235-51.

3. Schwartz IB, Billings L, Bollt EM. Dynamical epidemic suppression using stochastic prediction and control. Physical Review E 70 (4): Art. No. 046220. OCT 2004

4. Stark J, Hardy K. Chaos. Useful at last? Science 301, 1192-1193, 2003.

5. Yingcun Xia, Ottar N. Bjørnstad, and Bryan T. Grenfell Measles Metapopulation Dynamics: A Gravity Model for Epidemiological Coupling and Dynamics The American Naturalist, volume 164 (2004), pages 267-281

6. Ellner SP, Bailey BA, Bobashev GV, Gallant AR, Grenfell BT, Nychka DW. Noise and Nonlinearity in Measles Epidemics: Combining Mechanistic and Statistical Approaches to Population Modeling. American Naturalist, Vol. 151, No. 5 (May, 1998) , pp. 425-440

7. Hernández Cáceres JL, Hernández Martínez L, Pérez Monzón M, and García Domínguez L. Nonlinear properties of measles epidemic data assessed with a Kernel Nonparametric Identification approach. Electron J. Biomed 2006:2 (en prensa). Available at http://biomed.uninet.edu/2006/n2/caceres.html

8. Tong H. Nonlinear Time series Analysis. Oxford University Press, 1990.

9. Lopes da Silva FH, Blanes W, Kalitzin SN, Parra J, Suffczynski P, Velis DN. Dynamical diseases of brain systems: different routes to epileptic seizures. IEEE Trans Biomed Eng. 2003 May; 50(5):540-8.

10. Pijn JP. 1990 Quantitative Evaluation of EEG Signals in Epilepsy, Ph.D. Thesis, Amsterdam University, Amsterdam. Lopes da Silva, F., Pijn, J. P., Boeijinga, P. 1989 Interdependence of EEG signals: linear vs. nonlinear associations and the significance of time delays and phase shifts. Brain Toper. 2, 9-18.

11. Pijn JP, Van Nerve J, Nest A, Lopes da Silva FH. Chaos or noise in EEG signals: dependence on state and brain site. Electroenceph clin Neurophysiol 79, 371-381, 1991

12. Pijn JPM, Velis DN, van der Heyden MJ, DeGoede J, Van Veelen CWM, Lopes da Silva FH. Nonlinear dynamics of epileptic seizures on basis of intracranial EEG recordings. Brain Topography 9, 249-270, 1997

13. Pereda E, Quian Quiroga R, Bhattacharya J. Nonlinear Multivariate Analysis of Neurophysiological Signals. (to appear in Progress in Neurobiology)

14. Pascual-Marqui R, Hernández-Cáceres JL, Biscay-Lirio R, Pérez L. "Study of EEG non linear correlation with application to epileptic activity". 1992. Third Meeting of the International Society for Brain Topography (ISBET) Amsterdam.

15. Duncan SR, Scott S, Duncan CJ. A demographic model of measles epidemics. Eur J Popul. 1999 Jun;15(2):185-98

16. Shope, RE. Global climate change and infectious diseases. Environmental Health Perspectives 1991; 96: 171-74.

Comment of the reviewer Douglas R McLean PhD. Lecturer in Mathematics and Statistics. Department of Computing Science and Mathematics. University of Stirling, Stirling. Scotland. UK.

This work concerns the analysis of fortnightly epidemiological data collected between 1944 and 1966 on 60 cities in England and Wales. The number of measles outbreaks is recorded per city per fortnight as is each city population. Ostensibly, the authors have applied a technique from neurophysiological brain scans to measles outbreaks in pre-vaccination Britain.

Measles outbreaks follow a markedly seasonal pattern and this work tries to estimate the time lag of measles epidemics between one city and another for all possible pairs of cities. The work is very promising, suggesting that the sea-port of Preston has played a leading role as the forerunner of disease spread. I feel the work is of some merit and could be published.

Comment of the reviewer Prof. Maykel Cruz Monteagudo. Applied Chemistry Research Center, Faculty of Chemical-Pharmacy. Department of Drug Design, Chemical Bioactive Center. Central University of Las Villas. Villa Clara. Cuba

Biostatistics constitutes at the present time a crucial tool in establishing the factors implicated in the characterization of any biological or natural phenomenon. In particular, the establishment of the nature of epidemics dynamics is a very complex task with a limited success until today due to the limitations of existing approaches for epidemics propagation. In the present paper the authors introduce the application of the nonlinear association approach introduced by P. J. Pijn for considering epidemics spread in a geographically distributed area representing a promising method of exploring spatial-temporal epidemics data. The most important contribution of the current paper in my opinion lies on the above mentioned which should be well pointed out in the title of the paper.

In addition, is creditable to note the potentialities of the method presented for the identification of forerunner cities of epidemics outbreaks in a given geographical area with certain level of confidence if it is properly used.

Finally, the work developed by Cáceres et al. constitutes a nice example of the proper use of statistics in real life problems that should be known by the scientific community.

Corresponding Author:
Jose Luis Hernandez Cáceres
CECAM-ISCMH, Calle 146 esquina a 31
Cubanacán, Playa, Ciudad Habana, Cuba. cacerjlh @ cecam.sld.cu

Received: March 24, 2006. Recceived reviewed: July 16, 2006.
Published, August 10, 2006.

PRE VACCINATION MEASLES OUTBREAKS IN ENGLAND AND WALES: NONLINEAR ASSOCIATION ANALYSIS SUGGESTS A LEADING ROLE FOR PRESTON.

Jose Luis Hernández Cáceres, Maicel Pérez Monzón¹,
Luis Garcia Dominguez¹, Miguel Sautié Castellanos,
Lourdes Hernández Martinez², and Eduardo Tejera Puente.

Center for Cybernetics Applications to Medicine CECAM-ISCMH
and Havana Agricultural University¹. Havana, Cuba.
Hospital for Sick Children², Montreal, Canada.

cacerjlh @ cecam.sld.cu

Rev Electron Biomed / Electron J Biomed 2006;2:34-45.

PRE VACCINATION MEASLES OUTBREAKS IN ENGLAND AND WALES: NONLINEAR ASSOCIATION ANALYSIS SUGGESTS A LEADING ROLE FOR PRESTON.

Jose Luis Hernández Cáceres, Maicel Pérez Monzón1, Luis Garcia Dominguez1, Miguel Sautié Castellanos, Lourdes Hernández Martinez2, and Eduardo Tejera Puente.

Center for Cybernetics Applications to Medicine CECAM-ISCMH and Havana Agricultural University1. Havana, Cuba. Hospital for Sick Children2, Montreal, Canada.

cacerjlh @ cecam.sld.cu

Rev Electron Biomed / Electron J Biomed 2006;2:34-45.

Jose Luis Hernández Cáceres, Maicel Pérez Monzón¹,
Luis Garcia Dominguez¹, Miguel Sautié Castellanos,
Lourdes Hernández Martinez², and Eduardo Tejera Puente.

Center for Cybernetics Applications to Medicine CECAM-ISCMH
and Havana Agricultural University¹. Havana, Cuba.
Hospital for Sick Children², Montreal, Canada.