Indice del volumen Volume index
Comité Editorial Editorial Board
Comité Científico Scientific Committee
- En ellos no existe la proporcionalidad causa-efecto, ya que pequeños estímulos pueden conducir a grandes respuestas.
- No es sencillo mediante su simple observación directa arribar a las variables que predeterminan el comportamiento del sistema. Este está determinado por los atractores que los influyen.
Un atractor es el punto o conjunto de puntos hacia el cual evoluciona un sistema si se le da tiempo suficiente como para hacerlo. Existen atractores tanto hacia estados de normalidad como de alteración de la misma (estados patológicos).
- Los sistemas complejos se caracterizan por tener muchos componentes y por que su comportamiento no se puede predecir basándose meramente en el conocimiento de sus componentes individuales. Crean circuitos donde las salidas terminan generando nuevas entradas, constituyendo sistemas cíclicos.
- Tienen la capacidad de auto-organización y la misma surge de la re-alimentación del sistema sin ayuda externa.
- Prigogine I. Las leyes del caos. Barcelona. Crítica. 1997
- Hayles K. La evolución del caos. Barcelona. Gedisa. 1993
- Lipsitz L, Goldberger A. Loss of complexity and aging. JAMA 1992; 267: 1806-1809
- Goldberger A. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. The Lancet 1996; 347: 1312-1314
- Editorials. Fractals and medicine. The Lancet 1991; 338: 1425-1426
- Lewin R. Complejidad. Barcelona. Metatemas: 1995
- Landsberg PT, Ludwig G, TOM R, Schatzman E, Margalef R, Prigogine I. Proceso al azar. Barcelona. Metatemas.1992
- Elbert T, Ray W, Kowalik Z, Skinner J, Graf KE, Birbauer N. Chaos and physiology: Deterministic chaos in excitable cell assemblies. Physiological Reviews. 1994; 74: 1-41
- Chaos Williams GP. Chaos Theory Tamed. Joseph Henry Press, Washington, 1997.
- Sussman GJ, Wisdom J, Mayer ME. Structure and Interpretation of Classical Mechanics. The MIT Press, Cambridge, Massachusetts. 2000.
- Gollub JP. Order and disorder in fluid motion. Proc. Natl Acad Sci, Vol 92, pp 6705-6711, July 1995.
- Mallat S. A Wavelet Tour of signal processing. Academic Press, 1998.
- Falconer K. Fractal Geometry: mathematical foundations and applications. John Wiley and sons, 1990.
- Murray JD. Use and abuse of fractals, in Mathematical biology. Springer, 2002
- Semmlow JL. Biosignal and Biomedical Image Processing, MATLAB Based Applications. Marcel Dekker, New York – Basel. 2004.
- Rosenblatt J, Stoughton B. Mathematical Analysis for Modeling. CRC Press.1999.
- Yip K, Holstein-Rathlou N. Chaos and non-linear phenomena in renal vascular control. Cardiovascular Research 1996; 31: 359-370
- Yip KP, Holstein-Rathlou NH, Marsh DJ. Chaos in blood flow
control in genetic and renovascular hypertensive rats. Am. J. Physiol.261
(Renal Fluid Electrolyte Physiol.30): F400-F408, 1991.
HIPOTESIS MEDICA
PATRONES HISTOLOGICOS GLOMERULARES COMO
ATRACTORES CAOTICOS
Musso C1, Bezic J1, Christiansen S3, Algranati L1
1Servicios de Nefrologia y 3Anatomía Patológica. Hospital Italiano de Buenos Aires.
National University of Entre Rios, Engineering School2. Argentina
carlos.musso @ hospitalitaliano.org.ar
Rev Electron Biomed / Electron J Biomed 2007;1:28-34
English version
Comentario del Profesor Jose Luis Hernandez Caceres, PhD. Center for Cybernetics Applications to Medicine (CECAM), La Habana. Cuba
Comentario del Profesor Fernando Tricas PhD. Facultad de Informática. Universidad de Zaragoza. Zaragoza. España
TEORÍA DEL CAOS
RESEÑA HISTÓRICA Y CONCEPTOS PRINCIPALES
Clásicamente la física Newtoniana ha estudiado los sistemas lineales. Estos sistemas se caracterizan por guardar una proporcionalidad lineal entre sus causas y sus efectos, en ellos a una determinada magnitud de estímulo le corresponde la misma magnitud de respuesta, de modo que a causas pequeñas corresponden respuestas pequeñas y viceversa.
Los sistemas lineales poseen un orden evidente y su comportamiento en general puede ser entendido mediante su observación directa, resultando relativamente sencillo el reconocimiento de las variables que lo predeterminan.
Sin embargo, en la naturaleza no abundan este tipo de sistemas, sino los sistemas caóticos o no lineales. Los primeros estudios al respecto fueron hechos por el físico francés Henri Poincaré, a fines del siglo XIX, quién fue pionero en comprender que el caos no es sinónimo de desorden, sino de complejidad que aparenta desorden.
Los sistemas caóticos se caracterizan por las siguientes peculiaridades:
CAOS Y ENTROPÍA
Las leyes de la Termodinámica establecidas por Rudolf Clausius y Lord Kelvin, determinan que la entropía (magnitud física que mide la parte de la energía que no puede utilizarse para producir trabajo) hace que el universo tienda a la disipación de la energía y al mayor desorden.
Sin embargo estas aseveraciones no explican el surgimiento de la vida y su tendencia a la diversificación y complejización evolutivas: la aparición sucesiva de células, tejidos, órganos, sistemas de órganos, etc.
Maxwell trató de resolver esta incógnita mediante la siguiente hipótesis : si un sistema combatiese la disipación de su propio gradiente o entropía, podría explicarse entonces como logra el mantenimiento de su complejidad. Los científicos llamaron "neguentropía" o entropía negativa a esta actividad. Ilia Prigogine, uno de los fundadores de la Teoría del Caos, propuso que justamente la información que combate la entropía está representada por la auto-organización de la materia y la adquisición de un complejo orden interno, como sucede en los sistemas caóticos. De esta forma se puede explicar la evolución de la vida en armonía con los principios de la termodinámica.
LA GEOMETRÍA FRACTAL
Dentro de las ramas de la Teoría del Caos, hallamos la de la geometría de las cosas, desde la cual se intenta explicar las "caprichosas" formas de la naturaleza.
Para dicho fin el matemático Benoit Mandelbrot ha introducido el concepto de fractal, término que deriva del latín "fractus", que significa irregular o fragmentado.
Al fractal podríamos definirlo como un objeto geométrico cuya estructura básica se repite en diferentes escalas. Una de sus propiedades es la auto-similitud esto es, su forma parece similar en todas las escalas de amplificación. Este fenómeno es conocido como "simetría recursiva".
De esta forma los objetos fractales, que no pueden representarse por los cuerpos de la geometría clásica o Euclideana, (círculos, cuadrados, etc.), si pueden hacerlo por la iteración o repetición de una estructura básica (fractal).
Mandelbrot con su nueva geometrtía logra explicar la forma de mucho elementos de la naturaleza como es el caso de las costas marinas, las montañas, nubes, etc.
La geometría fractal se expresa por medio de algoritmos que requieren de una computadora para convertirse en formas y estructuras.
En una estructura fractal ésta adopta sistemáticamente una determinada morfología resultado de la iteración de una subestructura base.
En el cuerpo humano se han descripto estructuras fractales en las arterias coronarias, el sistema cardionector, las cuerdas tendinosas de las válvulas cardíacas, las vías vasculares y bronquiales del pulmón, los vasos retinianos.
GEOMETRÍA FRACTAL Y ESTRUCTURA GLOMERULAR
A continuación vamos a exponer una hipótesis elaborada a partir del estudio de fotografías del nefrón y del glomérulo en particular, tanto en estado de normalidad como de enfermedad.
En el presente trabajo proponemos que el nefrón obedecería a una forma fractal cuya estructura primordial sería la función matemática sinusoidal (seno-coseno).
La repetición (iteración) de la función matemática sinusoidal, con distintas variaciones para cada región nefronal (cápsula de Bowman, túbulos contorneados, etc), permite la construcción de un nefrón completo. (Figura 1)
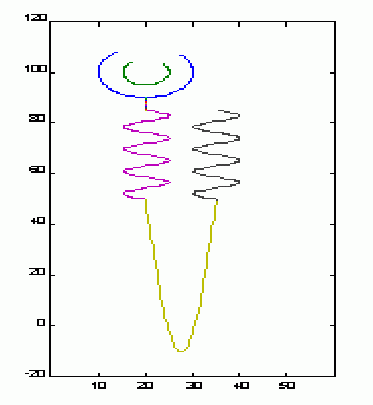
Figura 1

Además notamos que algunos patrones histológicos glomerulares, que se desarrollan en el contexto de diversas enfermedades, podrían también ser variaciones de la misma función matemática.
Tal es el caso de los patrones morfológicos de las glomerulopatías membranosa : espículas (Figura 2), membranoproliferativa: dobles contornos (Figura 3) y extracapilar: semilunas (Figura 4).
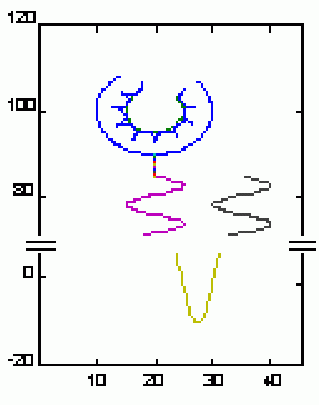
Figura 2

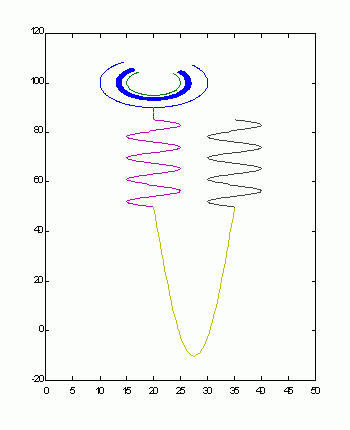
Figura 3

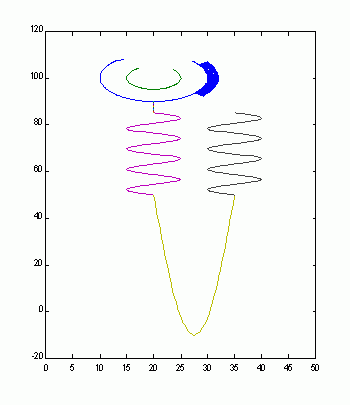
Figura 4

Sabemos que el glomérulo en estados de enfermedad sólo se deforma hacia un espectro limitado de opciones morfológicas, y que estos patrones histológicos no son privativos de una enfermedad, sino que distintas entidades renales confluyen en idénticos patrones glomerulares. Tal vez el glomérulo, ante las distintas noxas que lo agreden, pueda responder sólo con un limitado número de deformaciones, las cuales no serían azarosas sino determinadas por distintos atractores.
Concluímos que, desde la geometría fractal, la función sinusoidal podría explicar no solo la estructura nefronal normal, si no también la de algunos patrones histopatológicos glomerulares
Referencias
